Z検定と中心極限定理
ある集団から500人無作為抽出して得られた標本年齢データを用いる。
関西圏を中心に全国規模で展開しているある高齢者向けサービスでは会員の平均年齢は57.00歳であり、年齢の分散は36.91である。このたびD県にて新たにサービスを開始することになり、新規会員を募った。その新規加入者から500人を無作為抽出し、年齢を調べた(設定は架空)。
- 年齢の分散が全国と等しいものとするとD県新規加入者の平均年齢は何歳であると推定できるか。
- 全会員平均年齢57.00と今回調査対象者の標本平均57.56を比較してD県新規加入者の平均年齢は全国平均と異なっていると言えるか。
平均の差と確率
「ある集団の平均が特定の値(基準値)と異なっているかどうか」(A)を知りたい。ただしその際集団の本当の平均を知ることは出来ず、無作為抽出された一つの標本のみがあたえられているとする。無作為抽出は理論上は何回も出来、その都度そのときの標本平均が得られる。そして今回得られるのはそのたまたま抽出された一つの標本から得られた一つの標本平均である。
「基準値≠標本平均」であっても、標本平均ともとの集団(母集団)の平均には誤差があるため、A(「基準値と平均に差があること」)は確定しない。
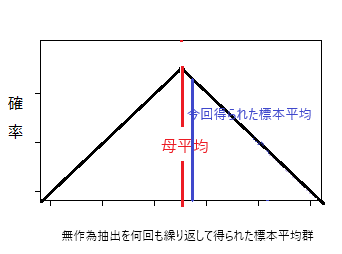
誤差を鑑みてもなお、標本平均と基準値が等しくなる可能性がなければ、Aは論証されたと言える。しかし標本調査において「可能性が0」になることはない。そこでその可能性が十分に小さければAは論証されたことにする。
一般的に言って平均差(←基準値-標本平均)が大きければ大きいほど標本平均=基準値となる可能性は減じるだろう。問題はどの程度平均差があれば「可能性が十分に低い」と言えるようになるのか、もし母平均が基準値と一致するとすると、標本平均が母平均とどれだけ離れた値を取れば、そんな値を取る標本が抽出される確率が十分に小さいと言えるのか、つまり平均差と確率との関係を知りたい。
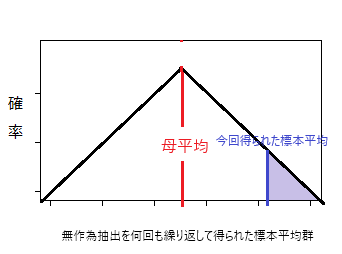
- x軸:無作為抽出を何回も繰り返して得られた標本平均群
- y軸:無作為抽出された標本の平均値(標本平均)が特定の値を取る確率
標本平均と母平均がそれだけの距離以上を持つ確率は図の色のついた部分の面積であたえられる。この面積=確率がP値であり、この値が一定(有意水準)以上小さければ「基準値≠標本平均」であると言えると定める。
中心極限定理
ここでわれわれが知りたいのはこの標本平均の分布である。そして無作為抽出を無限に繰り返した標本という設定をおけば、この標本平均の分布は確定するのだ。
実際に無作為抽出を繰り返し、その標本平均の分布をヒストグラムにしてみよう。
母集団年齢データを用いる。まずはこの集団(母集団)の年齢データのヒストグラムを描く。
mother <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/mother.csv", fileEncoding = "utf-8")
mother_age <- mother$年齢
source("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/socialStatisticsBasic.R", encoding="UTF-8")
descriptive(mother_age,width=2.5)
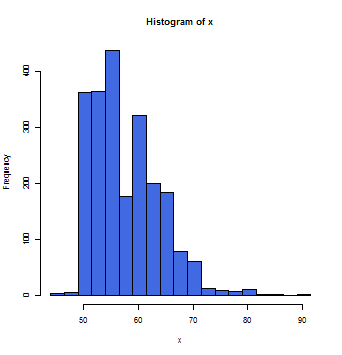
この集団からN件データを無作為抽出し、平均値を求めるという試行を10,000回繰り返す。
samplingTest(mother_age,N=1,10000)
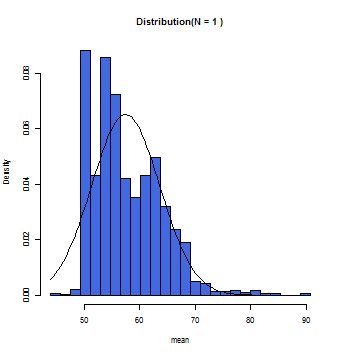
N=1の時は母集団の分布と近似した分布となる。
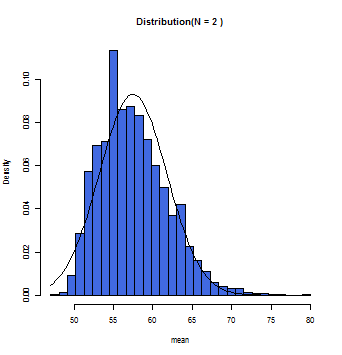
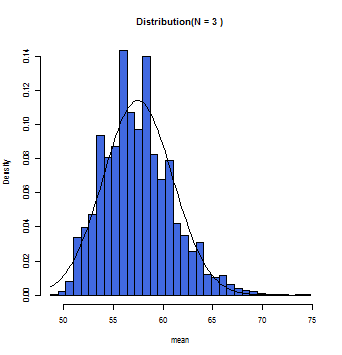
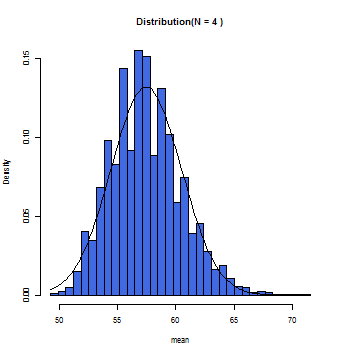
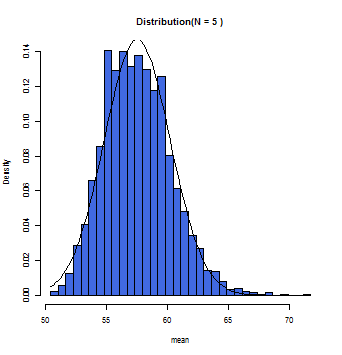
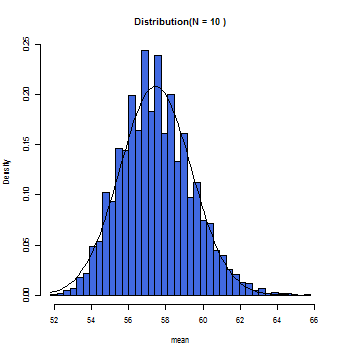
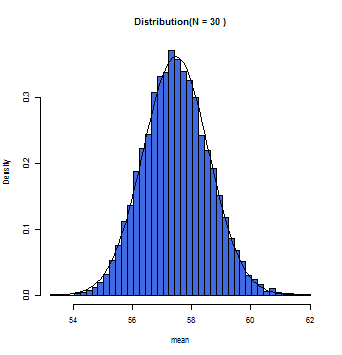
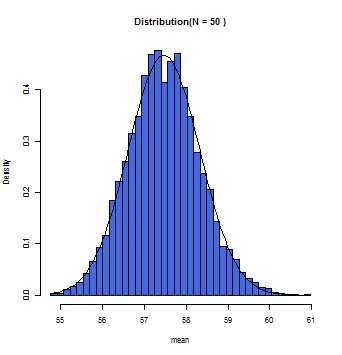
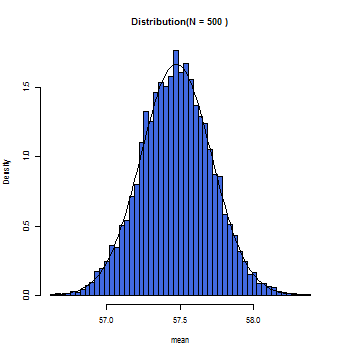
徐々にグラフ上の曲線とヒストグラムが一致していくのが分かるだろう。この曲線こそが正規分布曲線であり、この曲線において標本平均(x軸)とその確率(y軸)とが数学的に変換できるのである。
一般的にサンプルサイズが30(N=30)以上の時に標本平均の分布は正規分布に従う(中心極限定理)と仮定して構わないとされている。また母集団が正規分布であれば、Nの数にかかわらず、標本平均は正規分布に近似する。
標本平均の分布として正規分布をおくことが出来るのは
- 母集団が正規分布である。
- 母集団の分布にかかわらず、サンプルサイズが30以上である。
Z検定と区間推定
正規分布曲線は平均と標準偏差が決まれば確定する。
中心極限定理より
- 分布の平均=母平均
- 分布の分散=母分散/サンプルサイズ
分布の標準偏差=sqrt(母分散/サンプルサイズ)→「標準誤差」
年齢データから500件無作為抽出した時の標本平均の分布。
mother <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/mother.csv", fileEncoding = "utf-8")
mother_age <- mother$年齢
N <- 500 #サンプルサイズ500
num <- 10000 #試行回数
mean <- matrix(0,num,1)
for(i in 1:num){mean[i] <- mean(sample(x,N,replace=FALSE))}
#num回抽出を繰り返した時の標本平均の標準偏差
print(sd1 <- sd(mean))
curve(dnorm(x,mean=mean(mother_age),sd=sd1),from=56.5,to=58.5)
#標準誤差(=sqrt(母分散/サンプルサイズ))
print(sd2 <- sqrt(var(mother_age)/N))
curve(dnorm(x,mean=mean(mother_age),sd=sd2),add=T,col="red")
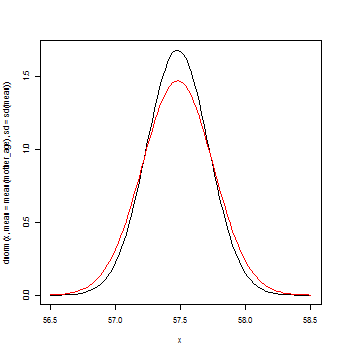
※標準誤差 > 十分な回数無作為抽出を繰り返した時の標本平均の標準偏差
標準誤差を用いたほうがなだらかな曲線(赤)になる。
標準正規分布
curve(dnorm(x,mean=0,sd=1),from=-3.5,to=3.5)
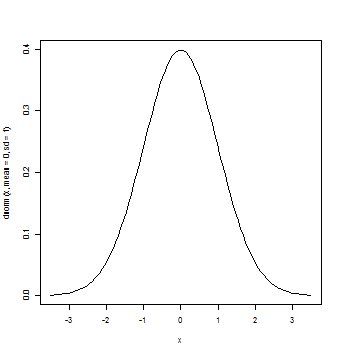
標準正規分布においては平均差と確率の関係が一意に決まる(数学的に計算される)。
| 有意水準α | Rでの計算式 | 概算 |
|---|---|---|
| 5% | qnorm(1 - 0.05/2) | 1.96 |
| 1% | qnorm(1 - 0.01/2) | 2.58 |
これを今見ているデータの正規分布の平均と標準偏差(標準誤差)に換算する。
Z検定
p値を計算する時には標準正規分布を用いる。そのために標本平均と母平均との距離を標準正規分布に換算した値がZ値である。Z検定ではこのZ値を検定統計量とする。
- 片側検定:p値(>)
-
サンプルの平均値が基準値より大きい値を取るときの確率 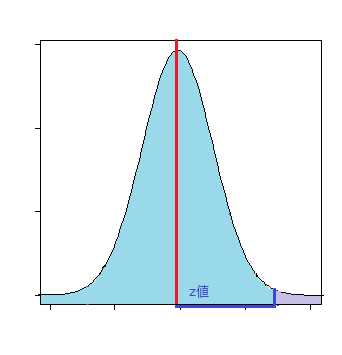
p <- 1 - pnorm(Z)
このp値が有意水準より小さいとき、「基準値>標本平均」と言える。
- 片側検定:p値(<)
-
サンプルの平均値が基準値より小さい値を取るときの確率 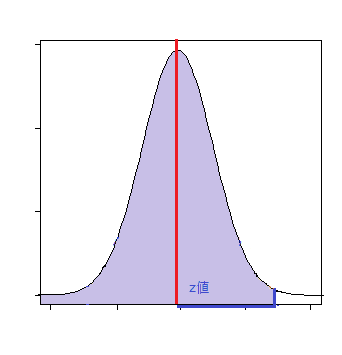
p <- pnorm(Z)
このp値が有意水準より小さいとき、「基準値<標本平均」と言える。
- 両側検定:p値(≠)
-
サンプルの平均値が基準値と異なる値を取るときの確率 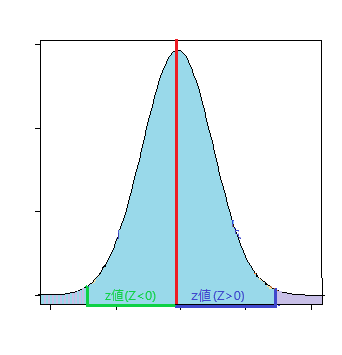
p <- (1 - pnorm(abs(Z)))*2
このp値が有意水準より小さいとき、「基準値≠標本平均」と言える。
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/age.csv", fileEncoding = "utf-8")
age <- data$年齢
mu <- 57 #基準値
sigma2 <- 36.91 #母分散
N <- length(age) #サンプルサイズ
#標準誤差
SE <- sqrt(sigma2/N)
#検定統計量Z
Z <- (mean(age) - mu) / SE
#p(= 基準値) 両側検定
(1 - pnorm(abs(Z)))*2
#p(> 基準値) 片側検定
1 - pnorm(Z)
#p(< 基準値) 片側検定
pnorm(Z)
区間推定
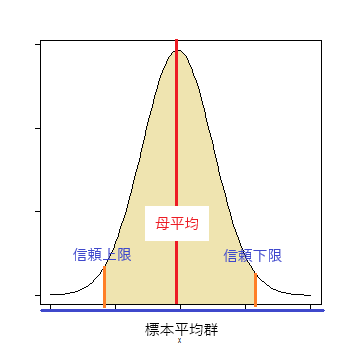
標本平均と基準値との距離が有意水準より大きい確率(オレンジ色の面積)内に収まる時、この平均値の範囲をもって「母平均の信頼区間」とする。
標本平均がオレンジ色の面積の左端に来た時、母平均(赤線)は上限となり、標本平均が右端に来た時、母平均は下限となる。
※この分布は標本平均の分布であって、母平均の分布ではない。
- 信頼上限 ← 標本平均 + 棄却値 * 標準誤差
- 信頼下限 ← 標本平均 - 棄却値 * 標準誤差
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/age.csv", fileEncoding = "utf-8")
age <- data$年齢
sigma2 <- 36.91 #母分散
N <- length(age) #サンプルサイズ
a <- 0.05 #有意水準
#標準誤差
SE <- sqrt(sigma2/N)
#棄却値
rejection <- qnorm(1 - a/2)
#信頼上限
mean(age) + rejection*SE
#信頼下限
mean(age) - rejection*SE
有意水準α=0.05としたとき、この信頼区間を95%信頼区間と呼ぶ。このときの95%とはA「母平均がその範囲に95%の確率で収まるであろう」ということを意味しない。そうではなくて、B「この信頼区間が母平均を含む確率が95%である」といっているに過ぎない。
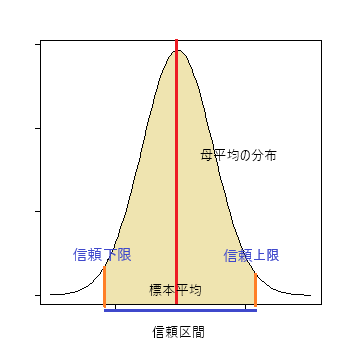
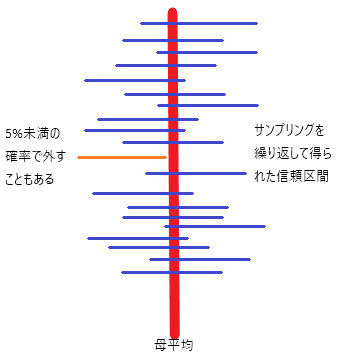
なにが違うのか?母平均に関する情報量はAの方が多いのである。残念ながらこの統計理論の枠組みでは母平均自体の確率云々は語り得ない。95%とは母平均に関する確率ではなくて、調査の精度に対する確率に過ぎないのだ。