一元配置要因分散分析
μ国B大学スマートフォン利用時間調査データ(架空データ)を用いる。
B大学の学生の中から500人を無作為抽出を行い、スマートフォン利用時間について調べたデータからスマートフォン利用時間に関する学部差を知りたい。
下記データより、B大学の学生のスマートフォン利用時間について、学部間の違いについてデータから得られる知見を述べよ。
| faculty | time |
|---|---|
| science | 193 |
| law | 166 |
| science | 293 |
| social | 215 |
| … | |
| science | law | social | literature | agriculture | economy |
|---|---|---|---|---|---|
| 205.32 | 169.44 | 18085 | 171.36 | 194.70 | 178.36 |

Fisherの分散分析
まずは2集団(社会学部と理工学部)の平均の差の検定をt検定とは異なるアプローチで行ってみる。理工学部・社会学部のみのデータを用いる。
| science | social |
|---|---|
| 205.32 | 18085 |

この結果から、理工学部と社会学部の利用時間の平均に差があると言えるかどうか。t検定とは別の考え方で検定を行う。
全体の平均値と個別学部の平均値との差に注目する。全体の平均値と個別の値との差に関する統計量は「分散」である。
分散比の比較
分散比のF検定を応用する。
一般的な分散(全体分散)を二つの分散に分解する。一つはStudentのt検定で用いられた集団内部での分散(残差分散)、もうひとつは集団間の分散(因子分散)である。
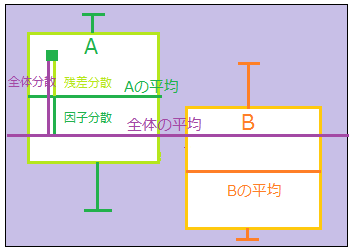
- 因子分散(集団間)
- 全体の平均からA,Bの平均までのばらつき
- 残差分散(集団内)
- AとBの共通分散
- Aの平均値からのA内の個々のデータ
- Bの平均値からのB内の個々のデータ
- 全体分散
- 全体の平均から個々のデータまでのばらつき
集団間の分散が大きいというのは、集団ごとの平均値が相互に離れているということである。その大きさが集団内部での分散(誤差由来)に比べて十分に大きければ、集団同士の平均値は離れていると言える。この集団間の分散(因子分散)と集団内部での分散(残差分散)との比をF検定で検証する。
- 因子分散 ← sum((集団iの平均 - 全体平均)^2×集団iのサンプルサイズ) / (集団の数 - 1)
- 残差分散 ← sum(集団iの偏差平方和) / sum(集団iの自由度)
- F ← 因子分散 / 残差分散
グループ間分散が大きくなればなるほどF値は大きくなり、グループの違いによる平均差が偶然では生じにくくなる。逆にグループ間分散が小さくなればF値は0に近づき、グループの違いによる平均差は偶然による誤差に飲み込まれる。この場合平均差に対するグループの違いの意味は小さくなる。
- 帰無仮説-「因子」が違うことは値の違いに無関係である(因子間で平均に差があるのは偶然だ)
- 対立仮説-因子によってこそ変動(平均からのズレ)は左右されているのであって、残差など文字通りのこりカスや!
- 因子による分散>>(圧倒的な、偶然とかケチの付けようのない差)>>残差による分散
F値が大きくなれば有意と一方向の検定なので片側検定である。
| 変動要因 | 変動SS | 自由度φ | 分散MS | F | P値(因子>残差) |
|---|---|---|---|---|---|
| 因子(因子間) | 25662.04 | 1 | 25662.039 | 6.69 | 1.04% |
| 残差(因子内) | 797344.29 | 208 | 3833.386 | ||
| 合計 | 823006.3 | 209 | 3937.829 | ||
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B-2.csv", fileEncoding = "utf-8")
summary(data)
value <- data$time
group <- factor(data$faculty)
#グループごとの平均
mean.group <- tapply(value,group,mean)
#グループごとのサンプルサイズ
N.group <- tapply(value,group,length)
#グループごとの自由度
df.group <- tapply(value,group,function(x){length(x)-1})
#グループの数
factor.N <- length(N.group)
#因子自由度
factor.df <- factor.N - 1
#残差自由度
residual.df <- sum(df.group)
#合計自由度
total.df <- length(value) - 1
#因子変動
factor.ss <- sum((mean.group - mean(value))^2*N.group)
#残差変動
residual.ss <- sum(tapply(value,group,function(x){sum((x -mean(x))^2)}))
#合計変動
total.ss <- sum((value - mean(value))^2)
#因子分散
factor.var <- factor.ss / factor.df
#残差分散
residual.var <- residual.ss / residual.df
#合計分散
total.var <- total.ss / total.df
#検定統計量F
f.value <- factor.var / residual.var
#p(> 基準値) 片側検定
1 - pf(f.value,factor.df,residual.df)
#効果量η2
factor.var*factor.df / (var(value)*total.df)
2集団での分散分析はStudentのt検定と全く同じ結果となる。t検定におけるt値を2乗したものがF値となる(逆にF値からはt値の符号は出てこない。つまりt検定における片側検定に相当することは出来ない)。
diff <- mean.group[[1]] -mean.group[[2]] se <- sqrt(residual.var/N[[1]] + residual.var/N[[2]]) t.value <- diff/se t.value^2 f.value
ここで使われている考え方は集団の数には依存しない。つまり3つ以上の集団間の平均差の有意性を扱うことが可能である。
1行目のみ下記データに変えても残りのスクリプトはそのまま利用できる。
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B.csv", fileEncoding = "utf-8")
summary(data)
この分析方法をFisherの分散分析と呼ぶ。
なおこの分析は各集団が等分散であることを前提とした分析であるため、集団間の分散の違いに対しては脆弱である。
Welchの修正
Fisherの分散分析に対して、各集団が非等分散であることに関して頑健性をもたせたものがWelchの修正分散分析である(t検定におけるStudentとWelch修正の関係と同じ)。実際の分析にはこのWelch修正を用いるのが良い。
計算の中身は理解不能。
- 因子自由度 ← 集団の数 - 1
- Welchの自由度(例のややこしい奴)
- 検定統計量F(…)
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B-2.csv", fileEncoding = "utf-8")
summary(data)
value <- data$time
group <- factor(data$faculty)
#グループごとの平均
mean.group <- tapply(value,group,mean)
#グループごとのサンプルサイズ
N.group <- tapply(value,group,length)
#グループごとの分散
var.group <- tapply(value,group,var)
#グループの数
factor.N <- length(N.group)
#因子自由度
factor.df <- factor.N - 1
rec.se2.group <- N.group / var.group
#Welchの自由度(相変わらずよくわからない)
welch.df <- (length(mean.group)^2 - 1)/(3*sum((1 - N.group/var.group/sum(rec.se2.group))^2/(N.group - 1)))
#検定統計量F(何をやっているのかはさっぱり)
welch.f.value <- sum(rec.se2.group*(mean.group - sum(rec.se2.group * mean.group)/sum(rec.se2.group))^2)/(factor.df*(1 + 2*(factor.df -1)/(length(mean.group)^2 - 1)*sum((1 - N.group/var.group/sum(rec.se2.group))^2/(N.group - 1))))
#p(> 基準値) 片側検定
welch.p.value <- 1 - pf(welch.f.value,factor.df,welch.df)
2グループの場合、Welchのt検定と同じ結果が得られる。
Rを用いた一元配置分散分析
#2学部の場合(上記説明に合わせたケース)
#data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B-2.csv", fileEncoding = "utf-8")
#本来の学部データ
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B.csv", fileEncoding = "utf-8")
summary(data)
x <- data$time
group <- factor(data$faculty)
#分散分析表
summary(aov(x~group))
#Fisherの分散分析結果
oneway.test(x~group,var.equal=T)
#Welch修正の分散分析結果
oneway.test(x~group)