単回帰分析
被験者諸属性と試験結果(架空データ)を用いる。
ある集団から無作為に選んだ326人に学力テストを行い、その点数を記録し、さらに受験者のさまざまな属性と合わせて結果を分析する。今回は得点と年齢の関係について考えを進める。
回帰分析とはある一つの量的変数の値について、一つないしは複数の変数との関係をモデル化する分析手法である。
最小二乗法と近似直線
散布図上に実測値(●)と直線(......)のy軸方向の残差(―)の二乗和を最小にするような直線を引く(最小二乗法)。
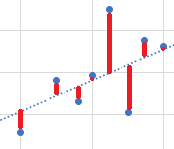
これが近似直線である。この直線の性質から変数間の関係を見ていくことになる。
相関係数自体はどちらの変数をx軸に持ってくるかは影響しないが、この直線に関してはどちらをxと置き、どちらをyと置くかで式は変わる。
| x | 独立変数 | 説明変数 |
| y | 従属変数 | 結果変数・目的変数 |
回帰分析では従属変数(結果変数)は一つ、独立変数(説明変数)は1つないし複数とる。
今回は年齢一つを説明変数とする。
散布図と相関係数
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/exam-result.csv", fileEncoding = "utf-8")
summary(data)
#サンプルサイズ
N <- length(data$no)
#点数と年齢の散布図(近似直線付き)
plot(marks~age,data)
lm.obj <- lm(data$marks~data$age)
abline(lm.obj,col=2,lw=2)
#点数と年齢の相関係数
r <- cor(data$marks,data$age)
#決定係数
R2 <- r^2
#無相関検定
cor.test(data$marks,data$age)
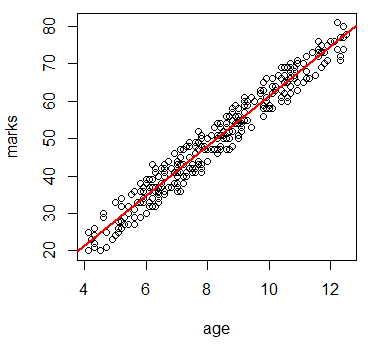
散布図からは年齢と点数には正の相関が見られる。年齢が高い時には点数も高い。相関係数とその検定でもその結果は裏付けられる。
相関係数を2乗した決定係数はデータ全体のばらつきに占める2変数が協調するばらつきの割合である。2変数の協調でデータのばらつきがどの程度説明できるかを示している。
回帰直線
回帰分析における近似直線を回帰直線と呼ぶ。回帰直線は傾きと切片によりあたえられる。独立変数が複数取れるので直線の式は一般に
y = a + b1x1 + b2x2 + … + bnxn
であたえられる。今回は説明変数は年齢のみなので
y = a + bx
切片aと傾きbは相関係数における近似直線と同じ。
#説明変数の偏差平方和 Sxx <- sum((data$age - mean(data$age))^2) #目的変数と説明変数の偏差積和 Sxy <- sum((data$marks - mean(data$marks))*(data$age - mean(data$age))) #傾き(回帰式) b <- Sxy / Sxx #切片(回帰式) a <- mean(data$marks) - b*mean(data$age) #目的変数の期待値(回帰式) expected.y <- a + b*data$age
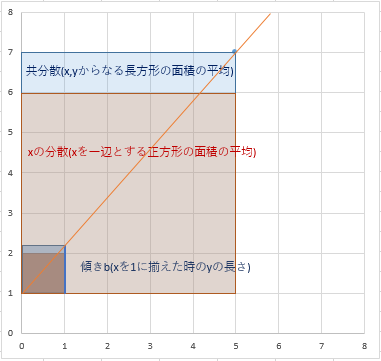

- 傾きbは長方形の面積(共分散)と正方形の面積(xの分散)の比である。
- 切片aは目的変数yの平均から長方形の縦の長さを減じたものである。
分散分析
#分散分析表 #変動 r.SS <- sum((expected.y - mean(data$marks))^2) #回帰変動-予測値と平均値とのズレ e.SS <- sum((data$marks - expected.y)^2) #残差変動-実測値と予測値とのズレ t.SS <- sum((data$marks - mean(data$marks))^2) #全体変動-実測値と平均値のとのズレ #自由度 r.df <- length(b) e.df <- (length(data$marks) - 1 - length(b)) t.df <- (length(data$marks) - 1) #分散 r.MS <- r.SS / r.df #回帰分散 e.MS <- e.SS / e.df #残差分散 t.MS <- t.SS / t.df #全体分散 #F検定 f.value <- r.MS / e.MS p.value <- 1 - pf(f.value,r.df,e.df)
- 回帰変動は1要因分散分析の因子(集団間)変動に相当
- 残差変動は1要因分散分析の残差(集団内)変動に相当
- 全体変動は1要因分散分析の全体変動に相当
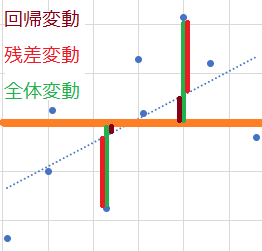
この分散分析の帰無仮説は「説明変数の変動によっては目的変数の値は変動しない」。因子分散(説明変数が因子となる分散)が残差分散に比べて十分に大きければ帰無仮説は棄却される。すなわち説明変数の変化によって目的変数も(一定)変化する、という結論が得られる。
回帰係数の有意性検定
#回帰係数の標準誤差 b.se <- sqrt(e.MS / (Sxx/t.df) / t.df) #回帰係数の有意性検定 b.t.value <- b/b.se b.p.value <- (1 - pt(abs(b.t.value),e.df))*2
- 回帰係数の標準誤差は「説明変数の分散(Sxx/t.df)が等しいとしたときの残差の分散(e.MS)の大きさ」を有効なデータの大きさ(合計自由度t.df)で割ったものの平方根である。
- 検定統計量tは「回帰係数b/標準誤差」
- 帰無仮説を「bが0と異なる値を取るのは偶然である」とする両側検定
このt検定により、bが0と異なる値を持つ、すなわち傾きを持つ、という結論が得られる。
標準化回帰係数
#標準化回帰係数 beta <- b*sd(data$age)/sd(data$marks)
傾きbの分母(説明変数の変動)・分子(目的変数の変動)を各々標準化した(x,yのばらつきの規模を揃えた)ものが標準化回帰係数。単回帰分析では標準化回帰係数は相関係数と一致する。