独立したサンプルのt検定
所属メンバーが異なっている2集団の平均の比較を行いたいときには「独立したサンプルのt検定」を行う。
μ国B大学スマートフォン利用時間調査データ(架空データ)を用いる。
B大学で学生の一日あたりのスマートフォンの利用時間を調査した。
B大学の学生の中から500人を無作為抽出を行い、スマートフォン利用時間について調査した。このデータからスマートフォン利用時間に関するジェンダー差を知りたい。
下記データより、B大学の学生のスマートフォン利用時間について、男子学生と女子学生の違いについてデータから得られる知見を述べよ。
Studentのt検定
これまでのt検定と同様、二つの集団の平均値の差が誤差の水準からして十分に大きければ有意とする。
1サンプルの時にはデータのばらつきも一つの標本のみを考えれば良かったが、2標本の時には各々のばらつきを扱わなければならない。そこが苦心のしどころ。
- 主張(対立仮説)
- グループの違いによって、個々の値が変わる(→その集約としての平均値が異なる)。
- 主張する際の障壁(帰無仮説)
- 個々の値はグループの違いとは別の理由によってばらついている(グループの違いなんて些細なこと)。
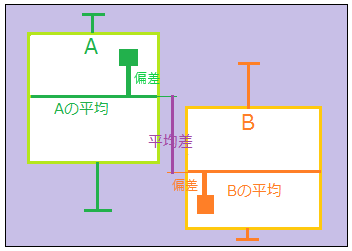
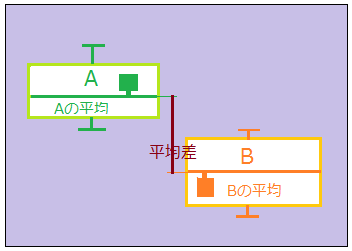
双方の集団内部でのばらつきが大きければ、集団間の平均差はばらつきの中に埋もれる。逆にばらつきが小さいと、平均差の意味が大きくなる。
集団1内でのばらつきの大きさと集団2内でのばらつきの大きさを足したもの(偏差平方和)が集団間の平均差の影響を排除したデータのばらつきの総量。それを2集団全体の自由度で割ったものが集団間の平均差の影響を排除した分散(共通分散)。
この共通分散を集団ごとにデータ数で割ったものが集団ごとのサンプルのばらつきで、それを足して平方根を取ったものが2集団全体の標準誤差となる。
標準誤差が求められた後はこれまでのt検定と同じ。平均差を標準誤差の水準で補正した値(検定統計量t)が、(偶然では生じえないほど)十分大きければ有意。
- 共通分散 ← (集団1の偏差平方和 + 集団2の偏差平方和) / (集団1の自由度 + 集団2の自由度)
- 標準誤差 ← sqrt(共通分散/集団1のサンプルサイズ + 共通分散/集団2のサンプルサイズ)
- 検定統計量t ← (集団1の平均値 - 集団2の平均値) / 標準誤差
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B.csv", fileEncoding = "utf-8")
summary(data)
male <- data$time[data$gender=="male"]
female <- data$time[data$gender=="female"]
diff <- mean(male) - mean(female)
df1 <- length(male) - 1
df2 <- length(female) - 1
df <- df1 + df2
#共通分散
v <- (sum((male - mean(male))^2) + sum((female - mean(female))^2))/df
#標準誤差
SE <- sqrt(v/length(male) + v/length(female))
#検定統計量t
t.value <- diff/SE
#p(!= 基準値) 両側検定
(1 - pt(abs(t.value),df))*2
#p(> 基準値) 片側検定
1 - pt(t.value,df)
#p(< 基準値) 片側検定
pt(t.value,df)
#効果量d
diff/sqrt((df1*var(male)+df2*var(female))/df)
#効果量r
sqrt(t.value^2/(t.value^2 + df))
※この検定法(Studentのt検定)は2集団の母分散が等しいことを前提としたものである。実際にはそうとは限らず、2集団の分散の違いに対しては脆弱な検定である。
そこで分散の違いに頑健(ロバスト)性を持たせた改良版t検定がWelchのt検定である。
Welchのt検定
改良版の分析法というのはもとの分析の原理的な含意を残した上で、ごにょごにょ調整を掛けて作られている(ことが多い)。その調整がどのようになされているのかはとりあえず置いておく(というか、ほとんどの場合私にもよく分からない)。
分散が異なっている以上、「共通分散」は想定しない。各々の集団の分散をそのまま使う。その分自由度(等価自由度)が複雑に計算される(この計算式が私には解説不能)。
- 標準誤差 ← sqrt(集団1の分散/集団1のサンプルサイズ + 集団2の分散/集団2のサンプルサイズ)
- 自由度←等価自由度(標準誤差と自由度の組合せで作られるなんだかとても複雑で理解不能な計算式)
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B.csv", fileEncoding = "utf-8")
summary(data)
male <- data$time[data$gender=="male"]
female <- data$time[data$gender=="female"]
diff <- mean(male) - mean(female)
#標準誤差
SE1 <- sqrt(var(male)/length(male))
SE2 <- sqrt(var(female)/length(female))
SE <- sqrt(var(male)/length(male) + var(female)/length(female))
df1 <- length(male) - 1
df2 <- length(female) - 1
#等価自由度
df <- SE^4/(SE1^4/df1+SE2^4/df2)
#検定統計量t
t.value <- diff/SE
#p(!= 基準値) 両側検定
(1 - pt(abs(t.value),df))*2
#p(> 基準値) 片側検定
1 - pt(t.value,df)
#p(< 基準値) 片側検定
pt(t.value,df)
#効果量d
diff/sqrt((df1*var(male)+df2*var(female))/(df1 + df2))
#効果量r
sqrt(t.value^2/(t.value^2 + df))
R標準関数を用いた独立したサンプルのt検定
Rではt検定には一般的にはt.test()関数を用いる。この関数は特別な指定をしなければWelchのt検定を行う。
どうしてもStudentのt検定を行いたいときには var.equal=T を指定する。
- t.test(formula, data, alternative="greater"/"less", var.equal=T/F)
-
- formula=「従属変数(検定変数:間隔・比例尺度)~因子(グループ化変数:名義尺度)」
- data=モデル中の変数を含むデータフレーム(formulaが実体を持つ時は省略可)
- alternative="greater"/"less" 片側検定の方向を指定する。
- var.equal=TRUE/FALSE 等分散を仮定するか否か(Fもしくは省略時はWelch検定、TならStudent検定を用いる)。
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B.csv", fileEncoding = "utf-8")
summary(data)
#Welchのt検定(≠)
t.test(time~gender,data)
#Welchのt検定(>)
t.test(time~gender,data,alternative="greater")
#Welchのt検定(<)
t.test(time~gender,data,alternative="less")
#Studentのt検定(≠)
t.test(time~gender,data,var.equal=T)
#Studentのt検定(>)
t.test(time~gender,data,alternative="greater",var.equal=T)
#Stundentのt検定(<)
t.test(time~gender,data,alternative="less",var.equal=T)
効果量は別途計算する必要がある。「社会統計用R自作関数」収録のt.test.independent()関数を用いると、効果量もまとめて算出する。