相関係数
量的な変数が複数ある時、この変数間の関係の強度を表す統計量が相関係数である。相関係数は関係の強さと方向性を示す。
被験者諸属性と試験結果(架空データ)を用いる。
ある集団から無作為に選んだ326人に学力テストを行い、その点数を記録し、さらに受験者のさまざまな属性と合わせて結果を分析することにした。
Aさんはその中から受験者の身長と試験結果との関連を分析し、「身長が高ければ、試験で高い点数を取れる」と結論付けた。
このAさんの分析を追試し、批評せよ。
| no | marks | height | age | gender |
|---|---|---|---|---|
| 1 | 50 | 122.06 | 8.6 | male |
| 2 | 76 | 153.21 | 12.0 | female |
| 3 | 43 | 117.53 | 7.2 | male |
| 4 | 51 | 127.56 | 8.4 | female |
| 5 | 30 | 109.83 | 6.0 | male |
| … | ||||
散布図
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/exam-result.csv", fileEncoding = "utf-8")
summary(data)
#サンプルサイズ
N <- length(data$no)
#点数と身長の散布図
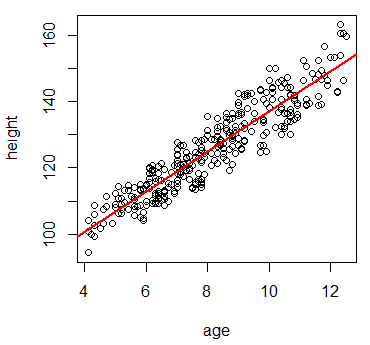
plot(marks~height,data)
lm.obj <- lm(data$marks~data$height)
abline(lm.obj,col=2,lw=2)
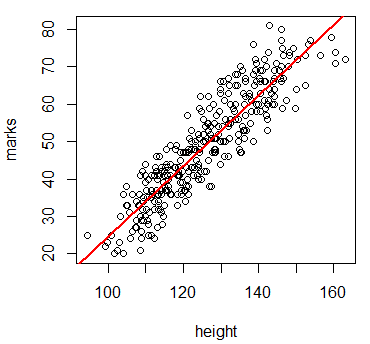
散布図からは身長の高さと点数には関係があるように見える。身長が高い時には点数も高い。この関係を「正の相関がある」という。
相関係数
偏差積和と共分散
#偏差積和 sum.of.products <- sum((data$marks - mean(data$marks))*(data$height - mean(data$height))) #共分散 cov <- sum.of.products/(N - 1)
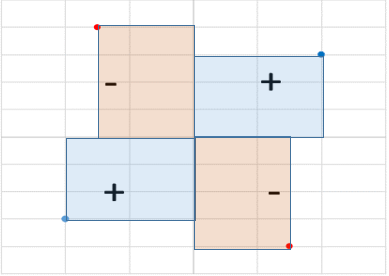
分散Varianceが1変数とその平均の差を一辺とする正方形の面積(偏差平方)の平均であるのに対して、共分散Covarianceは2変数の各々の平均との差を一辺とする長方形の面積(偏差積)の平均である。
ただし偏差積は負の値を取り得る。
相関係数
r <- cov / (sd(data$marks)*sd(data$height))
共分散は各々の変数の分散により、その大きさが変わる。それを統制し、各変数の散らばりの規模に依存しない値としたものが相関係数である。平均差を標準偏差で統制しているので、相関係数の絶対値は1を超えることはない。
もはや変数一つ一つの散らばりの規模には影響しない相関係数は変数1と変数2の関係に対する統計量となる。長方形の面積が正で占めれば相関係数も大きな値(<=1)となり、負で占めれば相関係数も小さな値(>=-1)を取る。また正負が拮抗すれば相関係数は0に近づく。
相関係数はサンプルサイズには依存しない統計量である。つまりこれは効果量と見なすことが出来る。
| 効果量rの絶対値 | 効果の目安 |
|---|---|
| 0.5 | 大 |
| 0.3 | 中 |
| 0.1 | 小 |
| 0 | なし |
相関係数の効果の目安はケースバイケースで判断するしかない。表は社会科学系での目安となる。自然科学系よりもrの数値が小さくても大きめの影響を見積もることが多い。
近似直線
相関係数が1または-1に近づく時というのはある直線にすべての実測値が重なる時である。このときこの直線を近似直線と呼ぶ。
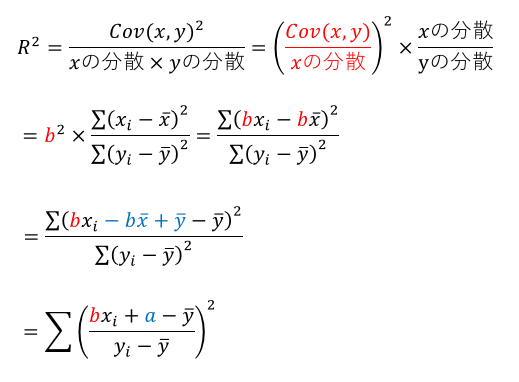
a+bx_i→y_i ならばR^2=1
つまり実測値(xi,yi)が直線
y = a + bx (a=mean(y) - b*mean(x), b=Cov(x,y)/var(x))
に接近すればするほど相関係数rは1または-1に近づく。
無相関検定
効果量はサンプルサイズの大きさにより、その有意性の判断は変わる。サンプルサイズが十分大きければ、効果量が小さな値でも有意となり得るし、サンプルサイズが小さければ、効果量が大きな値でも有意とならないかも知れない。有意性とは効果の大小とは別に、サンプリングによる偏りによってその効果が偶然的に生じうるのか否かを判断する指標である。
※仮に統計的に「有意」と判断できたとしても、効果があまりに小さければ、結果的にそれは意味が乏しいということも当然あり得る。統計的に有意だから「意味がある」というわけではない。
#自由度 df <- N - 2 #決定係数 r2 <- r^2 #標準誤差 se <- sqrt( (1 - r2) / df ) #検定統計量 t <- r / se #p値 p <- (1 - pt(abs(t),df))*2
- 相関係数の有意性を判断する際には、相関係数が二つの変数双方の平均値を規定のものとして求められているので、その分を差し引いたサンプルサイズ - 2が自由度となる。
- 相関係数を2乗した値を決定係数と呼ぶ。二つの変数双方の分散を掛け合わせたデータ全体のばらつきに対して2変数が協調するばらつき(共分散)の割合を示したものである。
- 1から決定係数を引いたものが相関関係の影響の外にあるデータのばらつき、すなわち残差となる。この残差をデータ量(自由度)で割り、平方根をとったものが相関係数の標準誤差である。
- 「相関係数が0と等しい」を帰無仮説とする無相関検定の検定統計量tは相関係数rを標準誤差で割ったものである。相関関係の標準誤差に対して相関係数が十分大きければ有意となるような値である。
- 後はおなじみのp値。「相関係数が0と等しい」を帰無仮説=「相関係数は0ではない」を対立仮説とするので両側検定。「相関係数が正または負である」ということを対立仮説とする場合は片側検定となる。
疑似相関と偏相関係数
成績と身長の相関係数は0.91、強い相関があり、サンプルサイズが326あるので、無相関検定でもp=0.00、有意。つまり成績と身長には正の相関がある。Aさんはさらに踏み込んで身長を「原因」と述べているのも「成績→身長」という因果は想定しづらい以上、妥当であろう。
え?ほんと!?身長が高ければ成績が上がる、という結論でいいの?
そういえば「朝食を取る生徒は成績がいい。だから朝食を食べよう」みたいなキャンペーンがあったなあ。あれもなんか怪しかったんだが。
そういえばこのデータ、点数と身長以外にも年齢という変数があったなあ。というか、このデータ、年齢を見てみれば子どものデータじゃん。
子どものデータなら年齢が高ければ身長も高くなるだろうし、得点も高くなる、というのはあり得そうだ。
#年齢と点数の散布図 plot(marks~age,data) lm.obj <- lm(data$marks~data$age) abline(lm.obj,col=2,lw=2) #年齢と身長の散布図 plot(height~age,data) lm.obj <- lm(data$height~data$age) abline(lm.obj,col=2,lw=2)
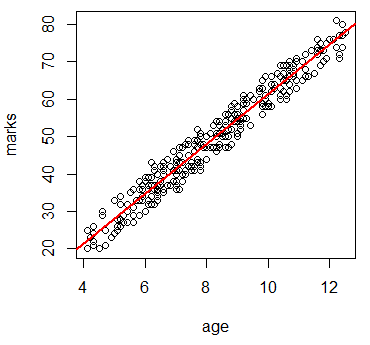
年齢と点数、年齢と身長の間に正の相関関係が見られる。
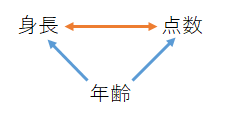
年齢→点数、年齢→身長という影響を排除して、点数と身長の相関を調べる
年齢によって点数が決まる、年齢で身長が決まる、双方の予測値(分散分析におけるカテゴリごとの平均値に相当)は近似直線によってあたえられる。そしてこの予測値と実測値の差が年齢の影響を排除した点数・身長の値(年齢からの残差)である。この年齢の影響を排除した点数・身長の値の相関を取ったものが偏相関となる。
近似直線は切片aと傾きbによって決まる。
#共分散 cov.ma <- sum((data$marks - mean(data$marks))*(data$age - mean(data$age)))/(N - 1) #点数~年齢 cov.ha <- sum((data$height - mean(data$height))*(data$age - mean(data$age)))/(N - 1) #身長~年齢 #傾きb b.ma <- cov.ma/var(data$age) #点数~年齢 b.ha <- cov.ha/var(data$age) #身長~年齢 #切片a a.ma <- mean(data$marks) - b.ma*mean(data$age) #点数~年齢 a.ha <- mean(data$height) - b.ha*mean(data$age) #身長~年齢 #残差(実測値 - 予測値) res.ma <- data$marks - (a.ma + b.ma*data$age) #点数~年齢 res.ha <- data$height - (a.ha + b.ha*data$age) #身長~年齢 #残差の相関係数=年齢で統制した点数と身長の偏相関係数 partial.cor.mh.a <- cor(res.ma,res.ha)
あれれ?相関が消えた!?
年齢の影響を排除した点数の残差と身長の残差の散布図を描いてみよう。
plot(res.ma~res.ha)
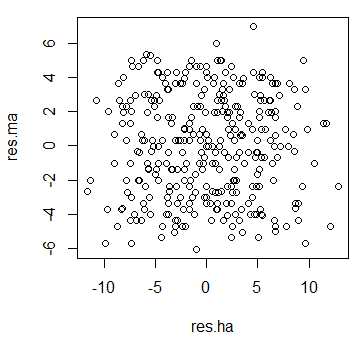
見事に相関が消えている。
年齢があがると身長と点数、双方が引き上げられ、結果として身長と点数にも正の相関関係が出てしまったということ。年齢が等しいもの同士では身長が高かろうが点数に影響が出ていない。このような相関を疑似相関と呼ぶ。
年齢の影響を排除して出てきた身長と点数の相関係数を「年齢で統制した身長と点数の偏相関係数 partial correlation coefficient」と呼ぶ。
点数、身長、年齢相互に正の相関があるから、年齢で統制すれば身長・点数の相関が消えるというのなら、同じく身長で統制すれば年齢・点数の相関も消えるの?
#共分散 cov.mh <- sum((data$marks - mean(data$marks))*(data$height - mean(data$height)))/(N - 1) #点数~身長 cov.ah <- sum((data$age - mean(data$age))*(data$height - mean(data$height)))/(N - 1) #年齢~身長 #傾きb b.mh <- cov.mh/var(data$height) #点数~身長 b.ah <- cov.ah/var(data$height) #身長~身長 #切片a a.mh <- mean(data$marks) - b.mh*mean(data$height) #点数~身長 a.ah <- mean(data$age) - b.ah*mean(data$height) #身長~身長 #残差(実測値 - 予測値) res.mh <- data$marks - (a.mh + b.mh*data$height) #点数~身長 res.ah <- data$age - (a.ah + b.ah*data$height) #年齢~身長 #残差の相関係数=身長で統制した点数と年齢の偏相関係数 partial.cor.ma.h <- cor(res.mh,res.ah) #身長で統制した点数と年齢の散布図 plot(res.mh~res.ah)
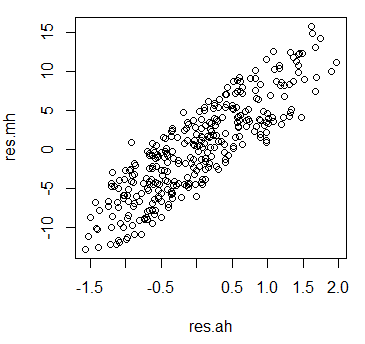
考察例
Aさんは身長と点数のみで相関係数を求めたが、Aさんは年齢と身長・点数の関係についての考察を行っていない。しかし年齢と身長・点数には非常に高い相関関係が見られた。
そこで身長と点数の関係を年齢で統制して、身長と点数の偏相関係数を求めた。
その結果、身長と点数の相関には有意差が出ない。つまり身長と点数は年齢を媒介とした疑似相関であると言える。このデータから読み取れる結論は「年齢が高い方が試験で高い点を取る傾向がある」と言うことである。
Aさんは疑似相関を真正の相関と見なしたところが間違っている。
Rでの相関係数
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/exam-result.csv", fileEncoding = "utf-8")
summary(data)
#点数と身長の相関係数
cor(data$marks,data$height)
#点数と身長に対する無相関検定
cor.test(data$marks,data$height)
#点数(2列目)、身長(3列目)、年齢(4列目)の相関行列
cor(data[2:4])