基本統計量
とあるグループの身長と年齢データ(excelCrossTab01.csv)を用いる。
基本統計量とヒストグラム
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/office/lesson/excel/excelCrossTab01.csv", fileEncoding = "utf-8") #データフレーム型のdataにcsvファイルデータを取り込む。
summary(data)
x <- data$身長 #xはベクトル
基本統計量の中でも特に重要なのが代表値とデータの散らばり(散布度)である。
- 代表値…分布上の位置を表す
-
- 平均値…比例・間隔尺度・
順序尺度・名義尺度 - 中央値…比例・間隔尺度・順序尺度・
名義尺度 - 最頻値…比例・間隔尺度・順序尺度・名義尺度
- 最大値…比例・間隔尺度・順序尺度・
名義尺度 - 最小値…比例・間隔尺度・順序尺度・
名義尺度
- 平均値…比例・間隔尺度・
- 散布度
-
- 範囲…最大値 - 最小値
- 分散…個々の値と平均値との偏差平方の平均
- 標準偏差…sqrt(分散)
この中では比例・間隔尺度における「最頻値」が厄介。順序尺度・名義尺度の時は単純に同じ値の数を数えれば最頻値が求められるが、比例・間隔尺度においてはそれではあまり実用にならない(Excelのmode関数)。一定の区切り幅の中で度数の高い区間から求める方が実用的である。
このような最頻値を求めるためにはまずは度数分布表を作ることが先決である。
度数分布表とヒストグラム
連続数を変数として度数分布表を作る時には、その変数を任意の区切り幅でカテゴリ―化するのが一般的である。今回は身長を5cm区切りで設定する。この区切りを「ビン」と呼ぶ。
#ビンの設定 start <- 140 end <- 185 width <- 5 cut <- seq(start,end,width) #cutはベクトル
このcutがビンとなる。cutには以下のような数値が入っている。
身長データxをこのcutで区切って度数分布表とヒストグラムを作成する。Rでは先にヒストグラムを作成するのが簡単。
hist <- hist(x,cut,right=FALSE,col="royalblue")
- hist(x,cut,right,col)
-
戻り値はリスト型
- x=ベクトルデータ
- cut=区切り(ビン)
- right=TRUE…「より大きい、以下」,FALSE…「以上、未満」のデータを同じ区切りとする
- col=色
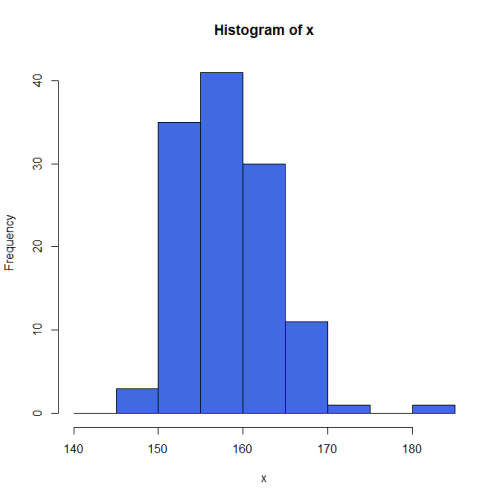
ExcelやSPSSでヒストグラムを作ると「right=TRUE」相当のものが出来る。それで構わないが、直感的な見やすさは「right=FALSE」の方であろう。
freq <- matrix(hist$counts) #freqは行列、hist$countsには度数データがベクトル型で入っている
rownames(freq) <- format(cut[-length(cut)],nsmall=2) #行列freqの行名を付ける
colnames(freq) <- c("freq") #行列freqの列名を付ける
hist$countsの中に度数データが入っている。
この度数データベクトルをmatrix(表)型にして、行ラベルに区切り(ビン)のラベルを指定する。ただし終端(185)は不要なので除去する。
| freq | |
| 140.00 | 0 |
| 145.00 | 3 |
| 150.00 | 35 |
| 155.00 | 41 |
| 160.00 | 30 |
| 165.00 | 11 |
| 170.00 | 1 |
| 175.00 | 0 |
| 180.00 | 1 |
統計量
以下、統計量を求めていく。Excelの関数とほぼ同等。
#身長の基本統計量 N <- length(x) mean <- mean(x) med <- median(x) mode <- mean(hist$mids[which(hist$counts == max(hist$counts))] )
最頻値(mode)は度数分布表よりもっとも度数の高い「26」(max(hist$counts))が含まれる区切り「155,160」の中央値となる。hist$midsが区切りの中央値データである。
| hist$counts | 0 | 2 | 18 | 26 | 17 | 7 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| hist$mids | 142.5 | 147.5 | 152.5 | 157.5 | 162.5 | 167.5 | 172.5 | 177.5 | 182.5 |
#身長の基本統計量続き max <- max(x) min <- min(x) range <- max - min V <- sum((x - mean)^2)/N sd <- sqrt(V) u2 <- var(x) u <- sd(x)
一般的な統計ソフト(除Excel)で普通に「分散」を求めると「不偏分散」が求められる。Rにおいてもvar()で求められるのは不偏分散(u2)である。記述統計においては定義通りの分散(標本分散)が本来。この分散はExcelではVAR.P関数で求められるものである。Rでは残念ながらそのような関数はない(はず)ので分散の定義から計算する。
分散
分散はデータの散らばり度合を表す統計量である。「範囲」と違って、全データの値を参照して算出される。
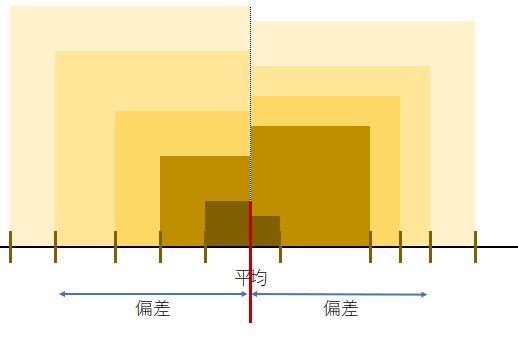
個々の値と平均値との差を偏差と呼ぶ。
この偏差を一辺とする正方形の面積が偏差平方であり、そのN個の正方形の面積の総和が偏差平方和である。
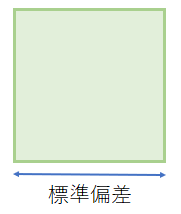
分散はこの偏差平方和を正方形の個数(N)で割ったものである。つまり正方形の面積の平均値が分散であり、その平方根を取ったもの(分散を面積とする正方形の一辺の長さ)が標準偏差である。
身長データ(x)から身長の平均値(mean(x))を減算したものの二乗和(偏差平方和)を求め、それをデータの大きさ(N)で除算する。
不偏分散
一般的な統計ソフトでは自身で計算しない限り不偏分散しか算出されない。記述統計の中ではそれは正確ではない。しかしそれはさほど問題ではない。
一般的に分散は値が大きい方が分析者にとって不利である(有意な結果が得られづらくなる)。不偏分散は定義通りの分散よりも値が大きくなる。それは*分析ゲーム*における胴元(分析者)がハンデを背負っているだけであり、分散を不偏分散で代用することはゲームのフェアさを損なわない。
※不偏分散を求めるvar関数はmatrixデータに対して用いると共分散行列を求める(sumやmeanとは異なる動きをする)。標準偏差を求めるsdはsum,meanと同じ動きをするので、そういう計算をしたい時にはsdで求めた値を2乗する。
グループ別基本統計量と箱ひげ図
カテゴリごとにグループ化されているデータを視覚化して比較したい時には度数分布表よりも箱ひげ図が便利である。
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/office/lesson/excel/excelCrossTab01.csv", fileEncoding = "utf-8") #データフレーム型のdataにcsvファイルデータを取り込む。
summary(data)
x <- data$身長 #xはベクトル
group <- factor(data$グループ) #groupを因子型にする
グループ化変数を設定し、それを基準に身長データを分割して、基本統計量を求める。
#グループ別基本統計量 N.group <- tapply(x,group,length) mean.group <- tapply(x,group,mean) median.group <- tapply(x,group,median) max.group <- tapply(x,group,max) min.group <- tapply(x,group,min) range.group <- max.group - min.group V.group <- tapply(x,group,function(x) sum((x - mean(x))^2)/length(x)) sd.group <- sqrt(V.group) u2.group <- tapply(x,group,var) u.group <- tapply(x,group,sd)
ある変数をグループに分割して計算したい時にはtapply関数を用いる。
- tapply(x,group,function)
-
- x=間隔・比例尺度のベクトルデータ
- group=グループ化変数(カテゴリ変数)
- function=関数定義または関数名
#グループ別箱ひげ図 boxplot(split(x,group),col="darkorange")

箱ひげ図はboxplot関数。引数はグループごとに分割された間隔・比例尺度データである。
- boxplot(var1,var2,…,col)
-
- var=間隔・比例尺度データ
- col=色
グループごとのデータ分割にはsplit関数を用いている。split関数の戻り値にはグループごとにラベルがつくので便利。
- split(x,group)
-
- x=間隔・比例尺度のベクトルデータ
- group=グループ化変数(カテゴリ変数)
$Berryz工房 [1] 153 150 164 166 159 159 182 161 $BEYOOOOONDS [1] 163.0 154.0 151.0 167.0 150.0 168.0 159.0 159.0 155.0 156.0 163.8 157.0 $`℃-ute` [1] 170.0 166.0 152.4 156.0 161.0 152.0 158.0 155.0 $`Juice=Juice` [1] 160.0 161.0 156.0 153.3 154.0 164.0 165.0 159.0 160.0 $アンジュルム [1] 162 159 155 153 159 162 154 161 162 153 163 166 152 160 163 154 160 152 $`カントリー・ガールズ` [1] 148 153 152 157 151 154 $こぶしファクトリー [1] 150.0 156.0 155.0 159.0 162.0 151.0 163.5 161.5 $つばきファクトリー [1] 159.0 155.0 160.2 157.5 167.0 153.0 162.0 153.2 160.0 $`モーニング娘。` [1] 158.0 160.0 167.0 152.0 149.0 157.0 145.0 158.0 159.0 155.0 163.0 153.0 155.0 153.0 156.0 156.0 154.0 156.0 [19] 156.0 156.0 153.0 167.0 154.0 168.0 153.0 163.0 157.0 155.0 152.0 160.0 150.0 156.0 159.0 152.0 157.0 157.0 [37] 166.0 164.0 162.0 152.5 152.0 155.0 161.0 159.0