一元配置反復測定分散分析
- 本章で用いる実習用ファイル
学力変化
S高校生徒の中から100人を無作為抽出を行い、入学後の学力の変化を調査した。
S高生の学力の変化ついて、データから得られる知見を述べよ。
| A | B | C | D | E | F | ||
|---|---|---|---|---|---|---|---|
| 1 | no | 入学時 | 1ヶ月後 | 2ヶ月後 | 3ヶ月後 | 4ヶ月後 | |
| 2 | 1 | 71 | 73 | 72 | 73 | 74 | |
| 3 | 2 | 71 | 72 | 72 | 72 | 73 | |
| 4 | 3 | 66 | 66 | 65 | 66 | 67 | |
| 5 | 4 | 62 | 62 | 62 | 63 | 63 | |
| μ国S高校学力推移調査データ | |||||||
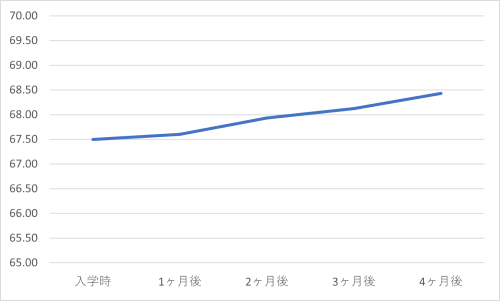
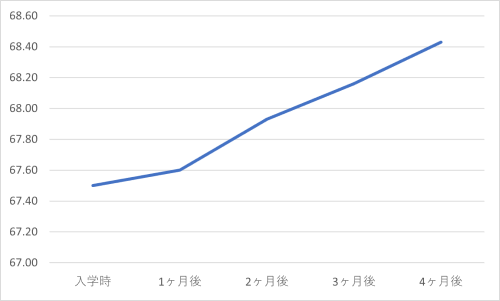
| 入学時 | 1ヶ月後 | 2ヶ月後 | 3ヶ月後 | 4ヶ月後 |
|---|---|---|---|---|
| 67.5 | 67.6 | 67.9 | 68.1 | 68.4 |
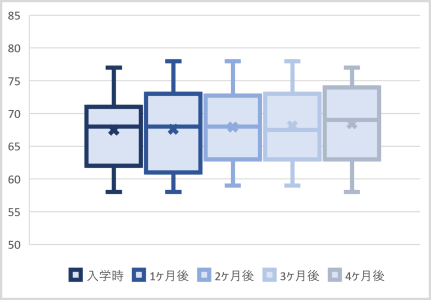
この結果より、学力の変化を読み取ることが出来るだろうか?
入学時より生徒の学力は伸びていると言えるのか、それとも偶然の範囲の変化に過ぎないのか?
反復測定分散分析
一元配置要因分散分析においては
- 個々の値 ← 全体の平均 + 要因ごとの平均差 + 誤差(残差)
で個々の値が説明された。データに対応関係があればそれにサンプルごとの平均差が加わる。
- 個々の値 ← 全体の平均 + サンプルごとの平均差 + 要因ごとの平均差 + 誤差(残差)
ある生徒のある回の成績は「全体の傾向+生徒の学力差+回ごとの成績差+誤差」で説明できると考える。
したがってここでは3つの分散を想定する。
- 要因分散
- 全体の平均と各期の平均とのばらつき
- サンプル分散
- 全体の平均と各サンプルの平均とのばらつき
- 残差分散
- 要因・サンプルによる変動では説明できない「誤差」
- 要因偏差を計算する。
各回の平均と全体の平均との偏差を求める。
A B C D E F G 1 no 入学時 1ヶ月後 2ヶ月後 3ヶ月後 4ヶ月後 平均 2 1 71 73 72 73 74 =AVERAGE(B2:F2) 101 100 63 62 63 64 64 63.20 102 平均 =AVERAGE(B2:B101) 67.60 67.93 68.12 68.43 =AVERAGE(B2:F101) 103 要因偏差 =B102:F102-G102 -0.32 0.01 0.20 0.51 - サンプル偏差を計算する。
各生徒の平均と全体の平均との偏差を求める。
A B C D E F G H 1 no 入学時 1ヶ月後 2ヶ月後 3ヶ月後 4ヶ月後 平均 サンプル偏差 2 1 71 73 72 73 74 72.60 =G2:G101-G102 3 2 71 72 72 72 73 72.00 4.08 101 100 63 62 63 64 64 63.20 -4.72 102 平均 67.50 67.60 67.93 68.12 68.43 67.92 - 残差偏差を計算する。
残差 = 個々の値 - 全体の平均 - サンプルごとの平均差 - 要因ごとの平均差
A K L M N O 1 no 入学時 1ヶ月後 2ヶ月後 3ヶ月後 4ヶ月後 2 1 =B2:F101-G102-H2:H101-B103:F103 0.72 -0.61 0.20 0.89 3 2 -0.58 0.32 -0.01 -0.20 0.49 4 3 0.42 0.32 -1.01 -0.20 0.49 101 100 0.22 -0.88 -0.21 0.60 0.29 - 各々の偏差平方和(変動)を求める。
R S 9 因子 変動 10 要因 =SUM(B103:F103^2)*COUNT(A2:A101) 11 サンプル =SUM(H2:H101^2)*COUNTA(B1:F1) 12 残差 =SUM(K2:O101^2) - 各々の自由度を求める。
R S T 9 因子 変動 自由度 10 要因 57.89 =COUNTA(B1:F1)-1 11 サンプル 16513.27 =COUNT(A2:A101)-1 12 残差 169.31 =COUNT(B2:F101)-T10-T11-1 - 各々の分散を求める。
R S T U 9 因子 偏差平方和 自由度 分散 10 要因 57.89 4 =S10:S12/T10:T12 11 サンプル 16513.27 99 12 残差 169.31 396 - 要因分散と残差分散の比(F値)を求める。
R U V 9 因子 分散 F 10 要因 14.47 =U10/U12 11 サンプル 166.80 12 残差 0.43 - 要因分散が残差分散より大きい値を取る確率p値を求める。
R T V W 9 因子 自由度 F p(要因>残差) 10 要因 4 33.85 =1-F.DIST(V10,T10,T12,TRUE) 11 サンプル 99 12 残差 396 - 効果量η2を求める。
R S X 9 因子 偏差平方和 η2 10 要因 55.89 =S10/SUM(S10,S12) 11 サンプル 16513.27 12 残差 169.31 効果量η2 効果の目安 0.14 大 0.06 中 0.01 小 0 なし
| 要因 | 偏差平方和 | 自由度 | 分散 | F | p値(要因>残差) | η2 |
|---|---|---|---|---|---|---|
| 要因 | 57.89 | 4 | 14.47 | 33.85 | 0.00 | 0.25 |
| サンプル | 16513.27 | 99 | 166.80 | |||
| 残差 | 169.31 | 396 | 0.43 | |||
一元配置要因分散分析との違い
一元配置反復分散分析は一元配置要因分散分析に「サンプルごとの平均差の効果」を足したものである。この差は分散分析表では残差変動・残差分散の差となって現れる。一元配置反復測定分散分析の方がサンプル効果を組み入れた分、残差が減る。F値の分母となる残差が減れば、有意性が出やすくなるというわけだ。
| 変動要因 | 変動 | 自由度 | 分散 | F | p |
|---|---|---|---|---|---|
| 時期 | 57.89 | 4 | 14.47 | 33.85 | 0.00 |
| サンプル | 16513.27 | 99 | 166.80 | ||
| 残差 | 169.31 | 396 | 0.43 | ||
| 変動要因 | 変動 | 自由度 | 分散 | F | p |
|---|---|---|---|---|---|
| 時期 | 57.89 | 4 | 14.47 | 0.43 | 0.79 |
| 残差 | 16682.58 | 495 | 33.70 | ||
主張
分散分析の結果から得られた知見をまとめよ。
-
入学時より4ヶ月かけて成績はわずかでも着実に上昇している(F(4,396)=33.85, p<.01, η2=0.25)。試験時期ごとの平均点の推移は図表1の通りである。全体の点数の変化はわずかではあるが、個々の点数は安定しており、一度身につけたスキルは確実に定着し、それを踏まえて次の礎としているのである。
図表1:成績推移 入学時 1ヶ月後 2ヶ月後 3ヶ月後 4ヶ月後 67.5 67.6 67.9 68.1 68.4