F検定
所属メンバーが異なっている2集団の分散の比較を行いたいときには「F検定」を行う。
男女別スマートフォン利用時間調査データ(架空データ)を用いる。
ある大学で学生の一日あたりのスマートフォンの利用時間を調査した。
男性と女性の学生を各々無作為で50人抽出し、一週間の平均利用時間を記録してもらった。
有効回答は男子学生が45人、女子学生は49人である。その結果をまとめたものが表である(架空調査)。
このデータから男子学生の利用時間と女子学生の利用時間で分散に差があると言えるか。
F分布
二つの集団の分散は比率で比較する。
F(分散比) ← 集団1の分散 / 集団2の分散
平均差の時には二つの集団が一致したときは0となるが、二つの集団の分散が等しい時はF = 1となる。
この分散比Fを検定統計量とする確率分布はχ2分布由来のF分布である。F分布は各々の集団の自由度により形が変わる。
curve(df(x,df1=1,df2=1),from=0,to=5,col=1) #黒 curve(df(x,df1=2,df2=2),from=0,to=5,add=T,col=2) #赤 curve(df(x,df=5,df2=5),from=0,to=5,add=T,col=5) #水色
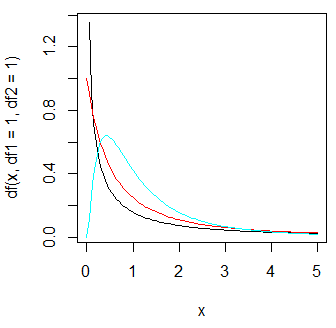
さらに自由度を増やすと
curve(df(x,df=50),from=0,to=100,lwd=3)
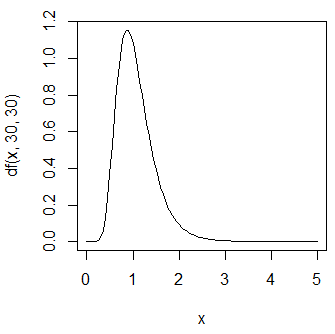
自由度が大きくなればF分布は正規分布に近似する。
F検定
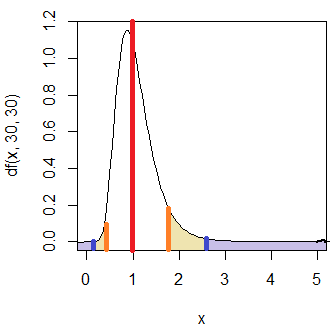
- 集団1の分散が集団2の分散と異なる値を持つ確率(青色のついた部分の面積)をp値(=)とする。このp値が有意水準より小さいとき、「集団1の分散≠集団2の分散」と言える(両側検定)。
- 集団1の分散が集団2の分散より一定以上大きい値を取る確率(青色のついた部分の右側面積)をp値(>)とする。このp値が有意水準より小さいとき、「集団1の分散>集団2の分散」と言える(片側検定)。
- 集団1の分散が集団2の分散より一定以上小さい値を取る確率(青色のついた部分の左側面積)をp値(<)とする。このp値が有意水準より小さいとき、「集団1の分散<集団2の分散」と言える(片側検定)。
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone05.csv", fileEncoding = "utf-8")
male <- data$利用時間[data$性別=="男"]
female <- data$利用時間[data$性別=="女"]
f.value <- var(male)/var(female)
#p(=) 両側検定
if(var(male) > var(female)){(1 - pf(f.value, length(male)-1,length(female)-1))*2}else{pf(f.value,length(male)-1,length(female)-1)*2}
#p(>) 片側検定
1 - pf(f.value, length(male)-1,length(female)-1)
#p(<) 片側検定
pf(f.value, length(male)-1,length(female)-1)
F検定の拡張
※三つ以上の集団間の分散の違いを検定したい時にはバートレット検定やルビーン検定が知られている。SPSSではルビーン検定が用いられている。
ルビーン検定は一元配置分散分析の応用で、変数を偏差の絶対値(abs(データ - 平均))に置き換えたものを用いて分散分析を行う。非正規型に対して比較的頑健性がある。
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone05.csv", fileEncoding = "utf-8")
value <- data$利用時間
group <- data$性別
center <- mean #medianを用いるとブラウン・フォーサイス検定になる(非正規型に対して頑健性が増す)
#グループごとの平均
mean.value <- tapply(value,group,mean)
#グループごとのサンプルサイズ
N <- tapply(value,group,length)
#偏差の絶対値の平均
mean.z <- tapply(value,group,function(x){mean(abs(x - center(x)))})
mean.z.mean <- sum(tapply(value,group,function(x){sum(abs(x - center(x)))}))/sum(N)
#自由度
factor.df <- length(mean.value) - 1
residual.df <- sum(N - 1)
#変動
factor.z.ss <- sum((mean.z - mean.z.mean)^2*N)
residual.z.ss <- sum(tapply(value,group,function(x){sum((abs(x - center(x))-mean(abs(x - center(x))))^2)}))
#分散
factor.z.var <- factor.z.ss / factor.df
residual.z.var <- residual.z.ss / residual.df
#検定統計量F
f.value <- factor.z.var / residual.z.var
#p(=) 分散は等しい
1 - pf(f.value,factor.df,residual.df)
Rにおける等分散検定
Rではバートレット検定がデフォルトで用意されている(ルビーン検定は'car' パッケージをインストールする)。
バートレット検定は非正規型に対して敏感な検定である。
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone05.csv", fileEncoding = "utf-8")
#バートレット検定
bartlett.test(data$利用時間~data$性別)
#ルビーン検定
install.packages("car", repos="http://cran.ism.ac.jp/") #一度インストールすれば後は不要
library(car)
leveneTest(data$利用時間~data$性別,center=mean) #center=meanの指定をしないとブラウン・フォーサイス検定