Rによる一元配置要因分散分析
所属メンバーが異なっている3集団以上の平均の比較を行いたいときにはt検定は用いることが出来ない。その場合は一元配置分散分析を行う。
μ国B大学スマートフォン利用時間調査データ(架空データ)を用いる。
B大学の学生の中から500人を無作為抽出を行い、スマートフォン利用時間について調べたデータからスマートフォン利用時間に関する学部差を知りたい。
下記データより、B大学の学生のスマートフォン利用時間について、学部間の違いについてデータから得られる知見を述べよ。
一元配置の分散分析を行う。その際、等分散性に対して頑健性が高いとされているWelch法(「平均値同等性の耐久検定」)を用いる。
またどのグループの平均差が有意なのかも調べる(多重比較)。多重比較には様々な手法があるが、その中で頑健性が高いとされているGames-Howell法を用いる(有名なのはTukeyだが、これは等分散性を前提とした分析である)。Games-Howel法は2グループ比較にWelch検定のロジックを用いているので、分散分析のWelch法とも整合している。
Rスクリプト
data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/smartphone00-B.csv", fileEncoding = "utf-8")
summary(data)
value <- data$time
group <- factor(data$faculty)
#一元配置分散分析と多重比較
source("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/socialStatisticsBasic.R", encoding="UTF-8")
output.anova <- oneway.factorial.anova(value~group,boxplot=T)
output.compare <- multiple.comparison.test(value~group, method="G")
#結果出力
output.anova
output.compare
#ファイルへの書き出し
write.output(output.anova,"output.anova.csv")
write.output(output.compare,"output.compare.csv")
oneway.factorial.anova関数(socialStatisticsBasic.Rで読み込まれる自作関数)
- oneway.factorial.anova(formula,data,boxplot=bool,col=col)
-
- formula=「従属変数(検定変数)~因子(グループ化変数)」
- data=モデル中の変数を含むデータフレーム(formulaが実体を持つ時は省略可)
- boxplot=箱ひげ図を出力するか(TRUE/FALSE 初期値はFALSE)
- col=棒の色(省略時はdarkorange)
multiple.comparison.test関数(socialStatisticsBasic.Rで読み込まれる自作関数)
- multiple.comparison.test(formula,data,method=method,summary=bool)
-
- formula=「従属変数(検定変数)~因子(グループ化変数)」
- data=モデル中の変数を含むデータフレーム(formulaが実体を持つ時は省略可)
- method=比較の方法("Games-Howell","Tukey","bonferroni","holm","BH")。
- bool=概要を出力するか(TRUE/FALSE 省略時はTRUE)
出力結果
一元配置分散分析
$summary
N df mean u2 Missing Value
agriculture 50 49 194.7000 3726.9490 0
economy 80 79 178.3625 560.9682 0
law 80 79 169.4375 1222.6290 0
literature 80 79 171.3625 4844.4366 0
science 150 149 205.3200 3076.5681 0
social 60 59 180.8500 5744.6720 0
Sum 500 494 185.8340 3223.8141 0
$anova
Sum Sq df Mean Sq F P eta2
Factor 105103.8 5 21020.754 6.906354 3.022874e-06 0.06533528
Residual 1503579.5 494 3043.683 NA NA NA
$test.result
F df1 df2 p eta2
Fisher 6.906354 5 494.0000 3.022874e-06 0.06533528
Welch 8.403800 5 189.7389 3.360555e-07 0.18130558
- 一元配置分散分析(Welch)
- F 8.403800
- df1 5
- df2 189.7389
- p 0.00
- 効果量
- η2 0.1813056
多重比較(Games-Howell法)
$`Games-Howell`
mean diff SE t df p
agriculture vs. economy 16.3375 9.030564 1.8091340 58.33259 4.680388e-01
agriculture vs. law 25.2625 9.477439 2.6655409 69.34487 9.556576e-02
agriculture vs. literature 23.3375 11.623013 2.0078700 114.20398 3.443589e-01
agriculture vs. science -10.6200 9.749330 1.0893056 77.74042 8.842250e-01
agriculture vs. social 13.8500 13.049273 1.0613618 107.88900 8.954706e-01
economy vs. law 8.9250 4.721754 1.8901873 138.88661 4.125446e-01
economy vs. literature 7.0000 8.219949 0.8515868 97.05375 9.567930e-01
economy vs. science -26.9575 5.246194 5.1384866 219.83365 9.012376e-06
economy vs. social -2.4875 10.136895 0.2453907 67.68736 9.998731e-01
law vs. literature -1.9250 8.708520 0.2210479 116.48794 9.999258e-01
law vs. science -35.8825 5.982752 5.9976584 221.65894 1.203541e-07
law vs. social -11.4125 10.536954 1.0830929 77.85706 8.866817e-01
literature vs. science -33.9575 9.003661 3.7715214 133.46062 3.256836e-03
literature vs. social -9.4875 12.501999 0.7588786 121.06466 9.737525e-01
science vs. social 24.4700 10.782161 2.2694895 85.43313 2.180554e-01
多重比較で有意なのは「経済学部」vs「理工学部」・「法学部」vs「理工学部」・「文学部」vs「理工学部」。
考察例
学部の違いによりスマートフォン利用時間に差があるかどうかを一元配置要因分散分析を用いて検証を行った。学部別の平均利用時間は以下の通りである。
| agriculture | economy | law | literature | science | social |
|---|---|---|---|---|---|
| 194.70 | 178.36 | 169.44 | 171.36 | 205.32 | 180.85 |
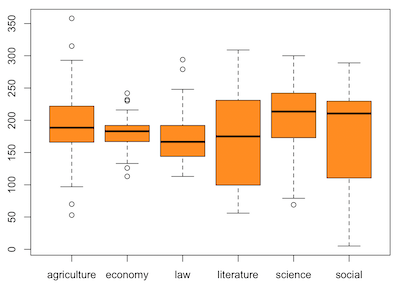
Welchの修正分散分析より、5%水準で有意差が見られた(F(5,189.74)=8.40, p<.001, η2=0.18)。
この結果より学部の違いによりスマートフォンの利用時間に差があると言える。
Games-Howell法により多重比較検定を行ったところ、「経済学部」vs「理工学部」(t(219.83)=5.14, p<.001)・「法学部」vs「理工学部」(t(221.66)=6.00, p<.001)・「文学部」vs「理工学部」(t(133.46)=3.77, p<.001)の間に有意差が見られた。