SPSS 基本統計量
基本統計量
とあるグループの身長と年齢データを用いる。
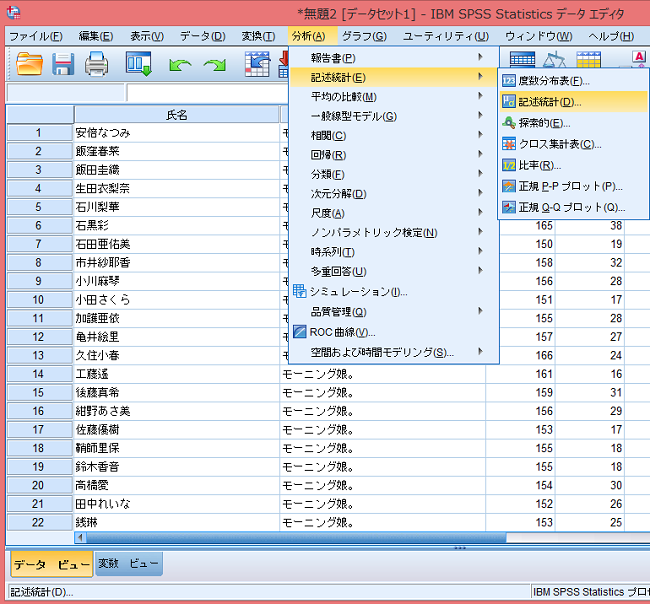
SPSSで基本統計量を求めるときには「分析(A)」→「記述統計(E)」→「記述統計(D)」。
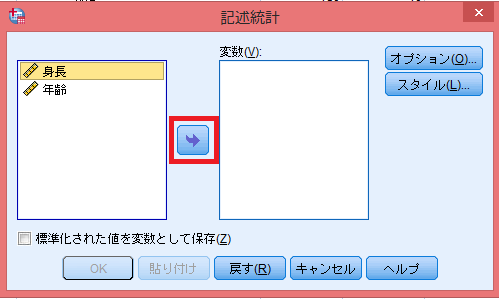
変数選択画面が出るので基本統計量を求めたい項目(変数)を選択する。複数選択もできる。
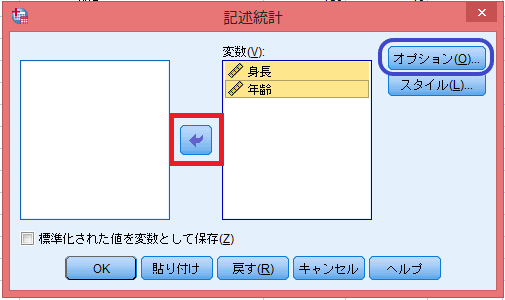
不要な変数は元に戻すことも出来る。
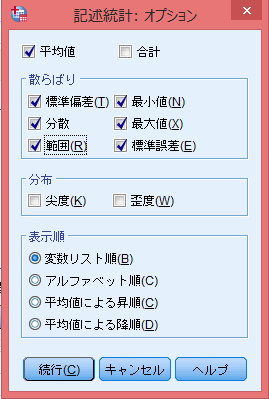
「オプション」画面より必要な統計量にチェックを入れる。
平均値・最小値・最大値・分散・標準偏差はチェックを入れること。
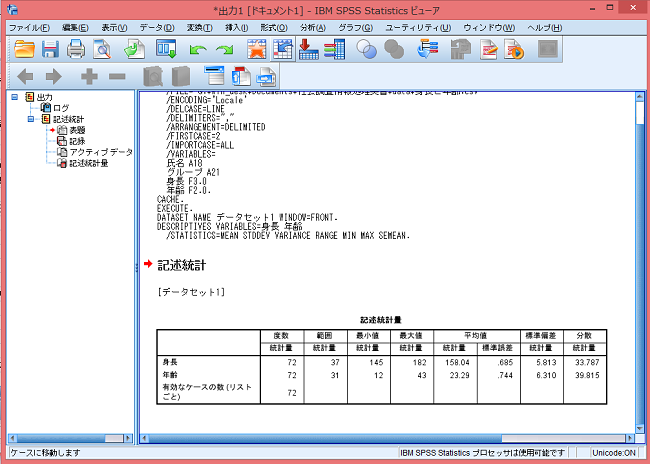
別ウィンドウが開いて、結果が表示される。
ただしこの方法では中央値medianが求められない(なんで?)。というので、別の道筋で基本統計量を求めてみる。
「分析(A)」→「記述統計(E)」→「探索的(E)」。
余計な図が出力されないように「表示」で「統計」を選択する。
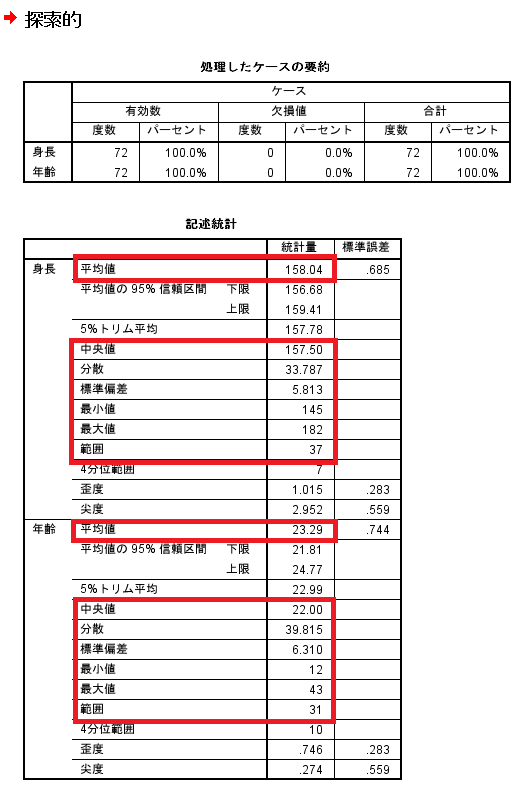
ビューアの出力結果に中央値を含め、基本統計量が出力される。
度数分布表とヒストグラム
連続数を変数として度数分布表を作る時には、その変数を任意の区切り幅でカテゴリ―化するのが一般的である。
連続変数のカテゴリー化
その際、SPSSではカテゴリー化した変数を新たに作成する。
「変数(T)」→「他の変数への値の再割り当て(R)」
カテゴリー化したい変数を選択する。今回は身長を5cm区切りで設定する。
「身長」を「入力変数」に選択する。
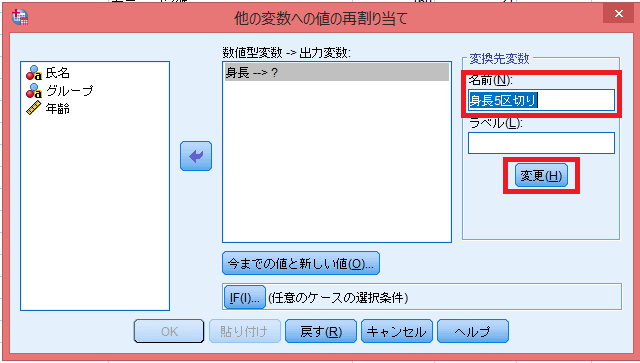
カテゴリー化した後の変数名を適宜決め(今回は「身長5区切り」)、「変換先変数」に入力し、「変更」ボタンを押す。
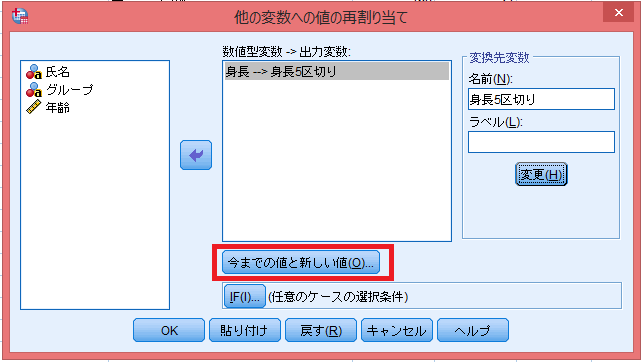
「今までの値と新しい値」ボタンを押す
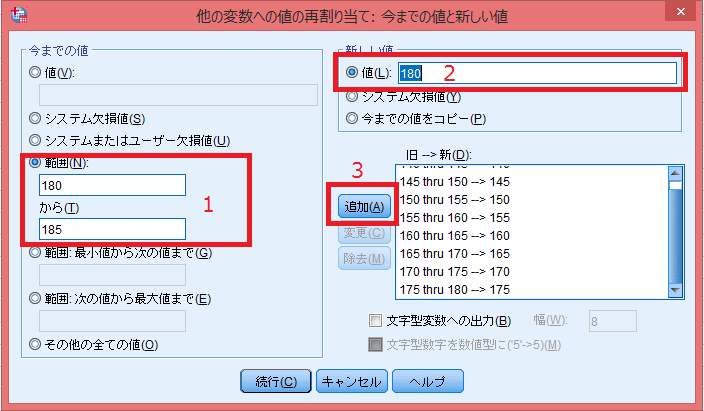
連続数の最小値から最大値まで全体をカバーするように、決めた区切り幅でのグループ化を行っていく。
- 「今までの値」→「範囲(N):」140「から(T)」145
- 「新しい値」→「値(L):」140
- 「追加」
を繰り返す。
※SPSSで「140から145」というのは140より大きく145以下の範囲になる。140はこの区切りには含まれないので注意。
最後に「続行」
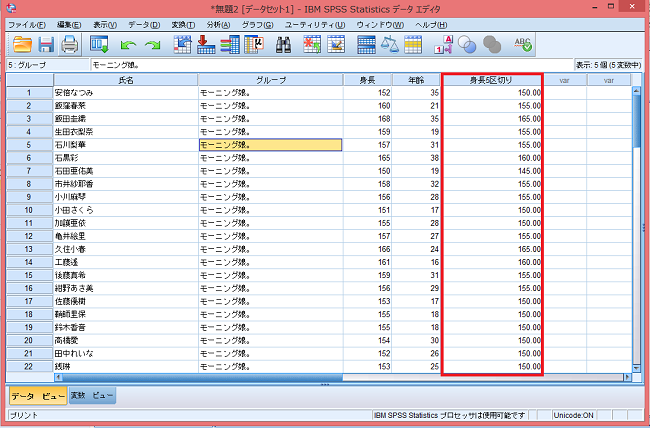
値再割り当て後の「データビュー」。
新たに作成した変数(「身長5区切り」)が登場する。
度数分布表・ヒストグラムの作成
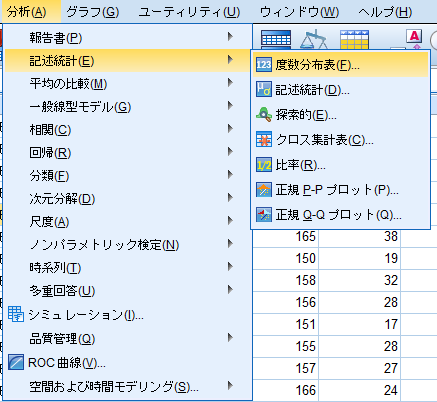
「記述統計(E)」→「度数分布表(F)」
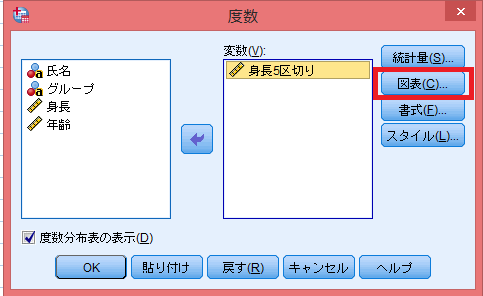
「再割り当て」で新たに作成した変数を選択する。
グラフ(ヒストグラム)も一気に作れる。「図表」より「ヒストグラム」
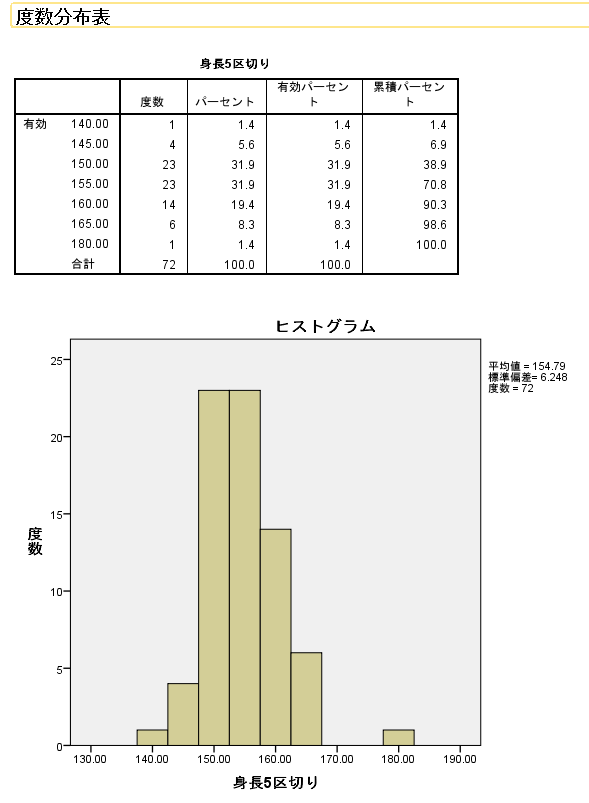
ビューアに出力された度数分布表とヒストグラム。
箱ひげ図
グループごとにデータの平均や分布・散らばりを比較したい時にはヒストグラムよりも箱ひげ図が便利である。
箱ひげ図は「記述統計(E)」→「探索的(E)」
「従属変数(D:)に量的データ、「因子(F:)」にグループ化変数を選択する。
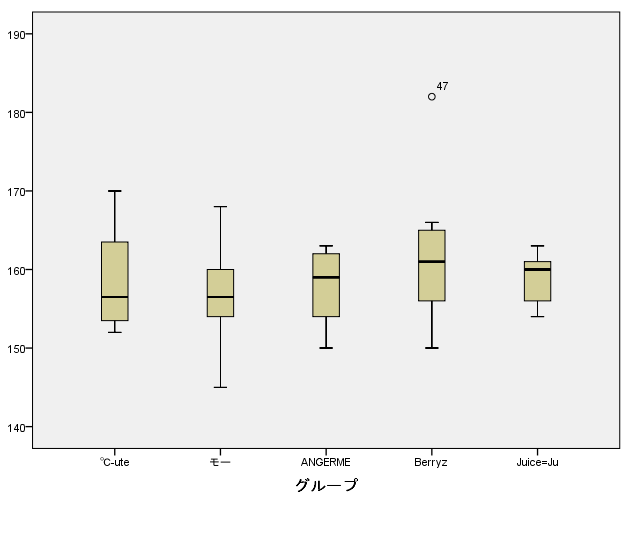
箱ひげ図が作成される。