統計講座

SPSS 一元配置要因分散分析

所属メンバーが異なっている3集団以上の平均の比較を行いたいときにはt検定は用いることが出来ない。その場合は一元配置分散分析を行う。

学部別スマートフォン利用時間調査データ(架空データ;UTF-8)を用いる。

ある大学で学生の一日あたりのスマートフォンの利用時間を調査した。

各学部の学生を各々無作為で50人抽出し、一週間の平均利用時間を記録してもらった。 有効回答は社会学部45人、文学部44人、経済学部43人、法学部54人、理工学部49人である。その結果をまとめたものが表である（架空調査）。

このデータから学部によってスマホ利用時間に違いがあると言えるか。

データの準備

再割り当て前

図では「利用時間」が検定変数、「学部」がグループ化変数である。

SPSSではグループ化変数（名義変数）の文字数が長いとエラーを起こすことがあるので、あらかじめ値の変換を行っておく。

「変換(T)」→「連続数への再割り当て(A)」

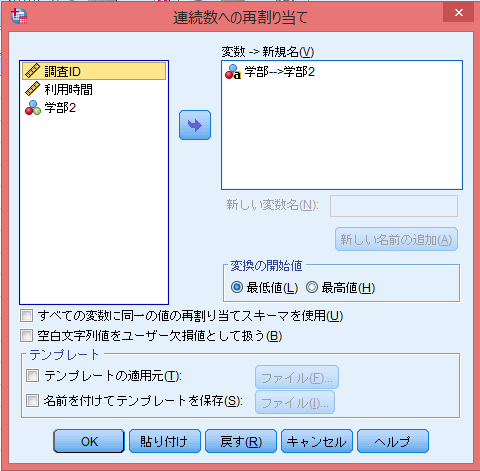
「変換(T)」→「連続数への再割り当て(A)」。

連続数への再割り当て

グループを識別するための変数を選択し、「新しい変数名」を適宜決める。

再割り当て後
  • 「社会学部」→「1」
  • 「理工学部」→「2」

    • と値が割り振られる。

    再割り当てを行った「学部2」をグループ化変数として用いる。

分析手順

「分析(A)」→「平均の比較(M)」→「一元配置分散分析(O)」

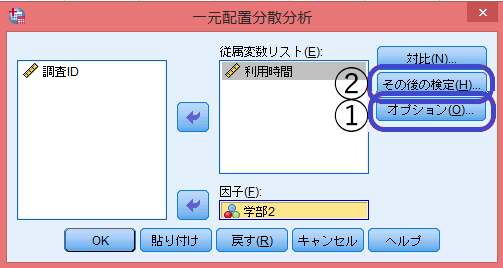
「分析(A)」→「平均の比較(M)」→「一元配置分散分析(O)」。

一元配置分散分析

比較する平均値を計算する元のデータを「従属変数リスト」に。集団を識別するカテゴリー変数を「因子」に選択する。この時先に変換した変数を選択する。

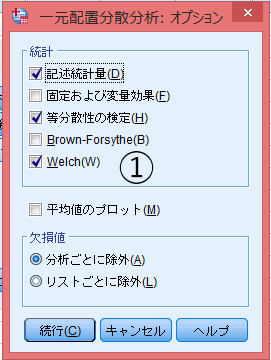
一元配置分散分析：オプション

等分散性に対して頑健性が高いとされているWelch法(「平均値同等性の耐久検定 Robust Tests of Equality of Means」)を用いる。「オプション」より「Welch」をチェック。

それ以外はお好みで。

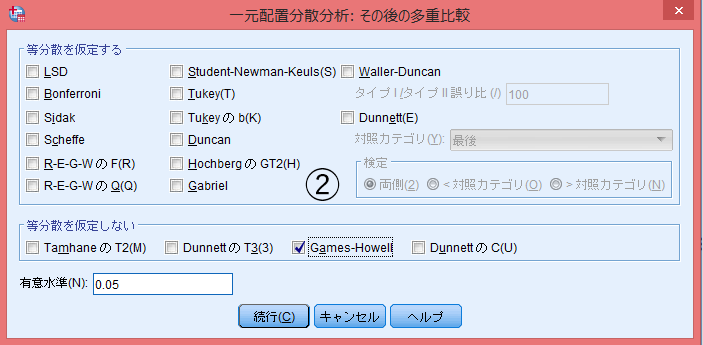
一元配置分散分析：その後の多重比較

分散分析で有意であれば、次に実際にどのグループの平均差が有意なのかを調べる(多重比較)。

多重比較には様々な手法があるが、その中で頑健性が高いとされているGames-Howell法を用いる(有名なのはTukeyだが、これは等分散性を前提とした分析である)。

「その後の検定」より「等分散が仮定されていない」→「Games-Howell(A)」をチェック。

出力結果

分散分析

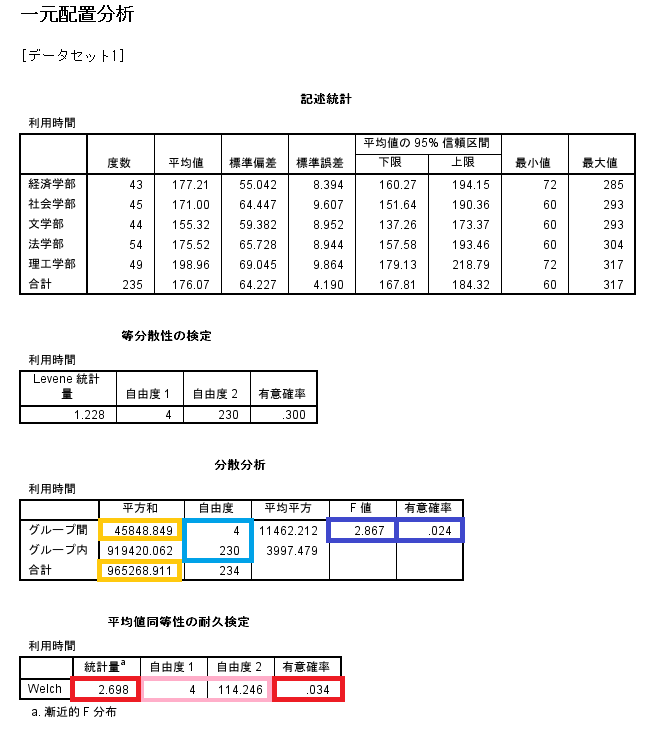
ビューアの出力結果・一元配置分析
Fisherの「分散分析」

各集団の分散が等しいことを仮定している。

  • 検定統計量F:「F値」2.867
  • 自由度df:「自由度」4と230。
  • p:「有意確率」.024
Welch修正(「平均値同等性の耐久検定 Robust Tests of Equality of Means」)

各集団の分散の違いに頑健な検定である。

  • 検定統計量F:「統計量」2.698
  • 自由度df:「自由度」4と114.246
  • p:「有意確率」.034
効果量
η2: グループ間平方和 / 合計平方和 → 0.048
効果量η2効果の目安
0.14大
0.06中
0.01小
0なし

多重比較

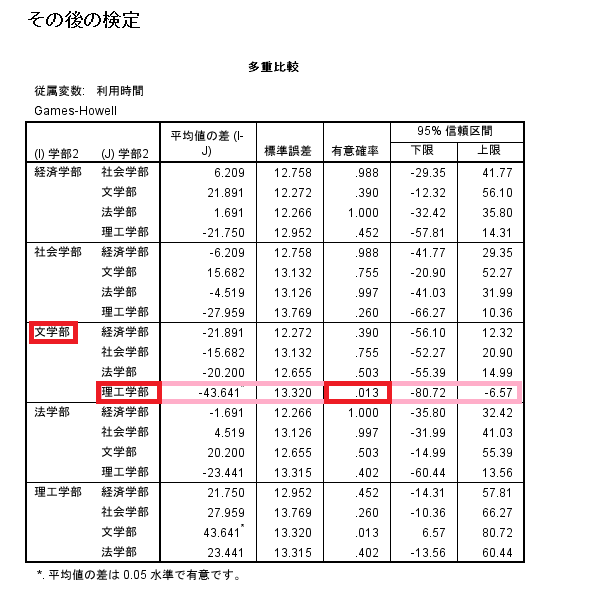
ビューアの出力結果・その後の検定

「有意確率」が0.05未満なら有意⇒多重比較で有意なのは「文学部」vs「理工学部」。

シンタックス

*「学部2」に連続数への再割り当て.
AUTORECODE VARIABLES=学部 
  /INTO 学部2 
  /PRINT.

*一元配置分散分析.
*記述統計・等分散性検定・Welch修正.
*欠損値は分析ごと.
*「その後の検定」はGames-Howell.
ONEWAY 利用時間 BY 学部2 
  /STATISTICS DESCRIPTIVES HOMOGENEITY WELCH 
  /MISSING ANALYSIS 
  /POSTHOC=GH ALPHA(0.05).

考察例

学部の違いによりスマートフォン利用時間に差があるかどうかを一元配置分散分析を用いて検証を行った。学部別の平均利用時間は以下の通りである。

経済学部177.21
社会学部171.00
文学部155.32
法学部175.52
理工学部198.96

Welchの修正分散分析より、5%水準で有意差が見られた（F(4,114.25)=2.70, p<.05, η2=0.05）。

この結果より学部の違いによりスマートフォンの利用時間に差があると言える。

この結果を踏まえてGames-Howell法により多重比較を行ったところ、理工学部と文学部の間に有意差が見られた(p<.05)。

SPSSでの分散分析の扱い

分析深度要因数等分散性SPSSの機能
要因分析
Factorial		一元配置
One-way		Fisher-前提「平均の比較」→「一元配置分散分析」
Welch-前提とせず「一元配置分散分析:オプション」→「統計」→「Welch」
二元配置
Two-way		前提「一般線形モデル」→「1変量」
反復測定
Repeated-Measures		一元配置
One-way		-Advanced Statisticsが必要
「一般線形モデル」→「反復測定」
二元配置
Two-way		Advanced Statisticsが必要
「一般線形モデル」→「反復測定」