統計講座

SPSS 平均の差の検定 1サンプル

ある標本の平均値がある基準値と異なっているかどうかの検証を行うときには「1サンプルのt検定」を行う。

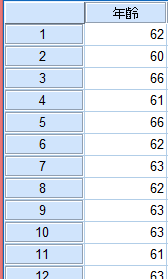
ある集団から500人無作為抽出して得られた年齢データを用いる。

定年退職者が集まって様々な社会活動を行っている団体で、メンバーの高齢化が話題となった。20年前はこの団体メンバーの平均年齢は57.00歳だったが、今はそれよりも年齢が高くなっているのではないかというのだ。そこでそのメンバーから500人を無作為抽出し、年齢を調べた（設定は架空）。

  • 現在のメンバーの平均年齢は何歳であると推定できるか。
  • 20年前の平均年齢57.00と今回調査対象者の標本平均57.56を比較して20年前に比べて現在高齢化が進んでいると言えるだろうか。

分析手順

年齢データ

なお分散も既知の時にはz検定を行うが、SPSSではz検定は機能として提供されていないようだ(本当？)。

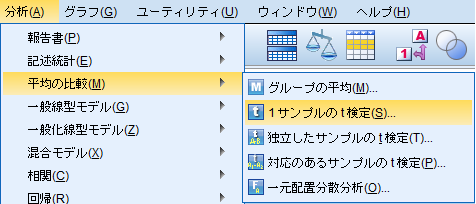
「分析(A)」→「平均の比較(M)」→「1サンプルのt検定(S)」

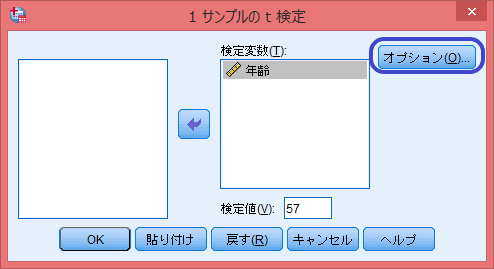
「分析(A)」→「平均の比較(M)」→「1サンプルのt検定(S)」。

1サンプルのt検定

「検定変数」に検定を行いたい標本データを選択。

比較対象の基準値を「検定値」に入力。

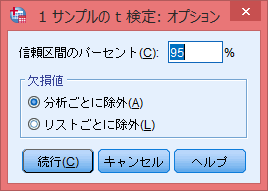
1サンプルのt検定　オプション

「オプション」で区間推定を行う際の信頼区間のパーセントを設定する。

信頼区間のパーセント = 1-有意水準α(5%ないし1%)

一般的には初期値の95%でよい。

出力結果

ビューアの出力結果(t検定)
区間推定
「差の95％信頼区間」。平均値の差がこの区間に収まる（信頼度95％）。
母平均の信頼区間は
  • 下限：検定値57 + 0.01 → 57.01
  • 上限：検定値57 + 1.11 → 58.11
平均の差の検定
  • 検定統計量t:「t値」1.983
  • 自由度df:「自由度」499
  • p(≠):「有意確率（両側）」.048
    p(>):有意確率（両側）.048 / 2 → .024
    ※今回の事例では現在の平均年齢が過去と比べて高くなっていることだけを懸念している。差があると言えないか、むしろ低い場合、いずれも懸念は解消される。
効果量
  • 効果量d: 「平均値の差」0.56 / 「標準偏差」6.315 → 0.09
  • 効果量r: SQRT(「t値」1,983^2/(「t値」1.983^2+「自由度」499)) → 0.09

シンタックス

* 1サンプルのt検定.
*変数→年齢.
*検定値→57.
*信頼区間のパーセント→.95.
T-TEST 
  /TESTVAL=57 
  /VARIABLES=年齢 
  /CRITERIA=CI(.95).

考察例

現メンバー年齢の区間推定を行った。95％の信頼区間で母平均は57.01<μ<58.11 である。

現メンバー平均年齢が過去平均(57.00)に比べて高くなっているかどうかを平均の差の検定を用いて検証を行った。

今回の調査で得られた標本の平均年齢は57.56であり、過去の平均年齢との差は0.56である。

t検定（片側）より5%の危険度でこの平均の差は有意である（t(499)=1.98, p<.05, r=0.09）。

この結果より現メンバーの平均年齢は過去平均より高いと言える。ただし効果量rより、この結果で顕著な差があるとは言えない。