統計講座

SPSS 平均の差の検定 独立したサンプル

所属メンバーが異なっている2集団の平均の比較を行いたいときには「独立したサンプルのt検定」を行う。

学部別スマートフォン利用時間調査データ(架空データ)を用いる。

ある大学で学生の一日あたりのスマートフォンの利用時間を調査した。

理系学部のほうが利用時間は長いのではないかと予想し、それを調べるため、社会学部と理工学部の学生を各々無作為で50人抽出し、一週間の平均利用時間を記録してもらった。

有効回答は社会学部が45人、理工学部は49人である。その結果をまとめたものが表である（架空調査）。

このデータから社会学部より理工学部のほうがスマホ利用時間が長いと言えるか。

値の再割り当て

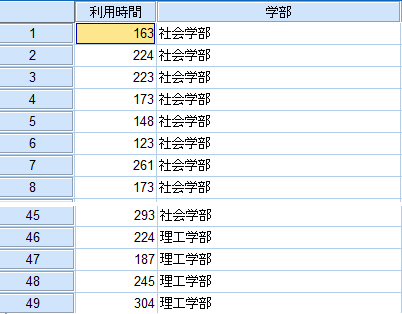
再割り当て前

図では「利用時間」が検定変数、「学部」がグループ化変数である。

SPSSではグループ化変数（名義変数）の文字数が長いとエラーを起こすことがあるので、あらかじめ値の変換を行っておく。

「変換(T)」→「連続数への再割り当て(A)」

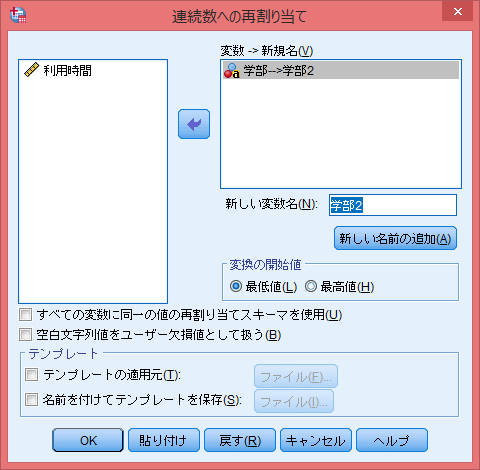
「変換(T)」→「連続数への再割り当て(A)」。

連続数への再割り当て

グループを識別するための変数を選択し、「新しい変数名」を適宜決める。

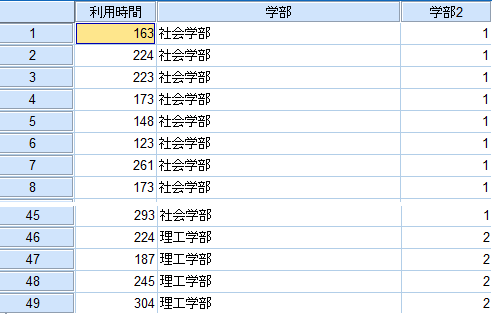
再割り当て後
  • 「社会学部」→「1」
  • 「理工学部」→「2」

    • と値が割り振られる。

    再割り当てを行った「学部2」をグループ化変数として用いる。

分析手順

「分析(A)」→「平均の比較(M)」→「独立したサンプルのt検定(T)」

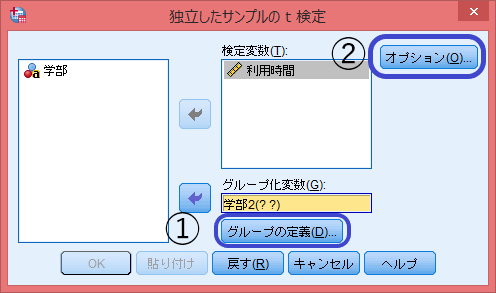
「分析(A)」→「平均の比較(M)」→「独立したサンプルのt検定(T)」。

独立したサンプルのt検定

比較する平均値を計算する元のデータを「検定変数」に。集団を識別するカテゴリー変数を「グループ化変数」に選択する。この時先に変換した変数を選択する。

グループの定義

「グループの定義」より比較したいグループの値を選択する。連続した数値データとなっているので「1」と「2」と入力する。

有意水準の設定は「オプション」から。一般的には初期値の.95でよい。

出力結果

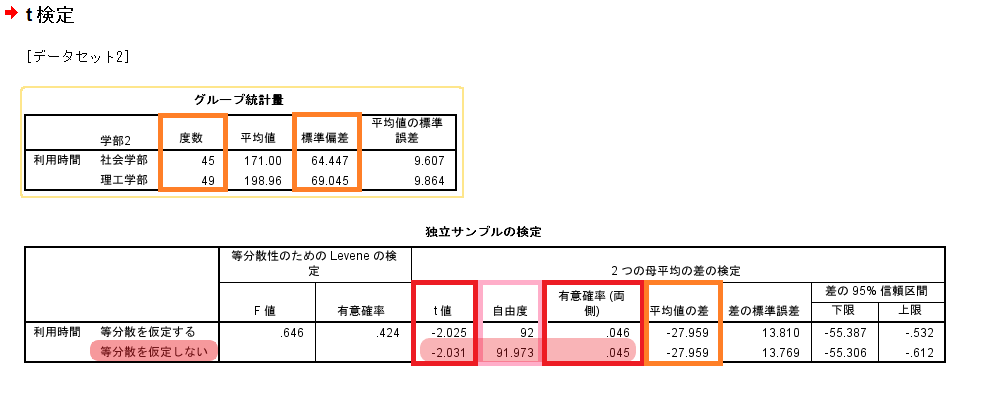
ビューアの出力結果(t検定)
平均の差の検定
Studentのt検定
「等分散を仮定する」
  • 検定統計量t:「t値」-2.025
  • 自由度df:「自由度」92
  • p(≠):「独立サンプルの検定」の「有意確率（両側）」.046
    p(<):.046/2→.023
Welchのt検定
「等分散を仮定しない」:2集団の分散の違いに対して頑健な検定である。
※Levene検定の結果を見て「等分散を仮定」するかどうか判断して検定法を変えるのは「検定の繰り返し」を招く。ここは黙ってより頑健なWelchを選ぶのみ。
  • 検定統計量t:「t値」-2.031
  • 自由度df:「自由度」91.973
  • p(≠):「独立サンプルの検定」の「有意確率（両側）」.045
    p(<):.045/2→.023
※社会学部のほうが利用時間が長いという結果が出たとしたら、それはそれで学部間文化を知る上で価値がある。「社会学部<理工学部」のみを検出するだけでは不十分であり、「社会学部>理工学部」も検出できる「両側」検定の結果を採択する。
効果量
  • 効果量d: 「平均値の差」-27.959 / SQRT((社会学部自由度44*社会学部「標準偏差」64.447^2+理工学部自由度48*理工学部「標準偏差」69.045^2)/「自由度」92) → -0.418
  • 効果量r: SQRT(「t値」2.031^2/(「t値」2.031^2+「自由度」91.973)) → 0.207

シンタックス

*「学部2」に連続数への再割り当て.
AUTORECODE VARIABLES=学部 
  /INTO 学部2 
  /PRINT.

*独立したサンプルのt検定.
*検定変数→利用時間.
*グループ化変数→学部2.
*信頼区間のパーセント→.95.
T-TEST GROUPS=学部2(1 2)
  /VARIABLES=利用時間 
  /CRITERIA=CI(.95).

考察例

社会学部の平均利用時間は171.00、理工学部の平均利用時間は198.96 であった。

社会学部と理工学部に利用時間に差があるといえるかどうかWelchのt検定(両側)を行ったところ、5%水準で有意差が見られた（t(91.97)=-2.03, p<.05, r=0.21）。

この結果より、社会学部より理工学部のほうがスマートフォンの利用時間は長いと言える。