統計講座

分析手順

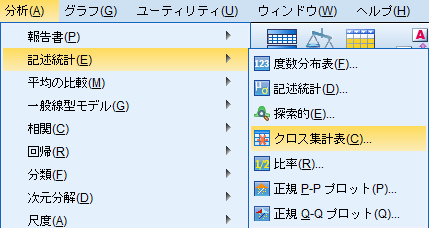
「分析(A)」→「記述統計(E)→「クロス集計表(C)」。

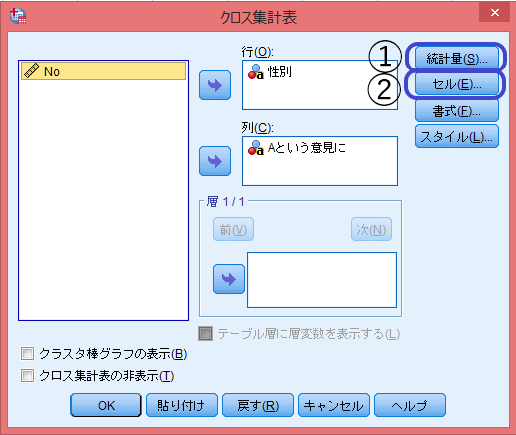
どちらを行、どちらを列にするかは文脈に依存する。

「統計量」「セル」を順に指定していく。

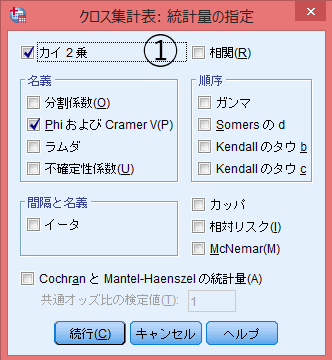
• 「カイ2乗」でクロス集計表の独立性の検定がされる。
• 「名義」→「PhiおよびCramerV(P)」が効果量。

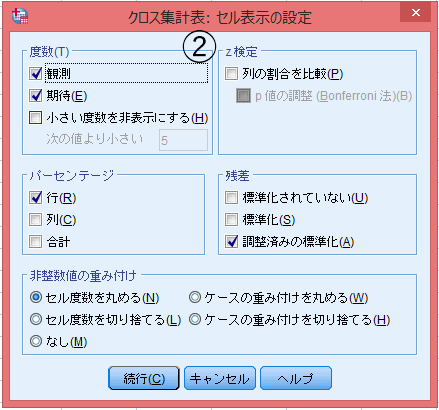
• 「度数」→「観測」・「期待」
• 「パーセンテージ」→文脈に依存する。今回は「行」に設定した性別ごとの傾向を見たいので「行(R)」。
• 「残差」→「調整済みの標準化(A)」。

結果

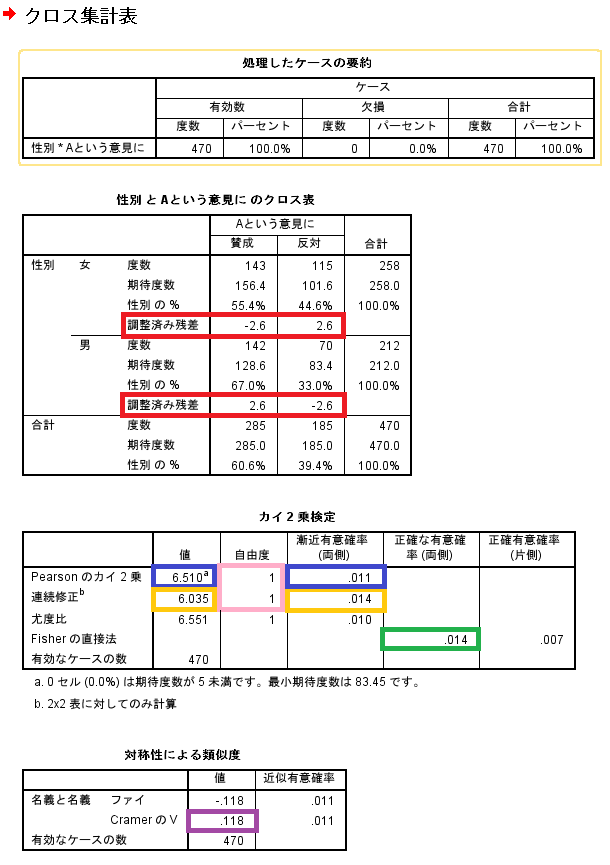
独立性の検定…「カイ2乗検定」

「Pearsonのカイ2乗」

• 検定統計量χ2:「値」6.510
• 自由度df:「自由度」は1
• p(≠):「漸近有意確率（両側）」.011

期待度数が5未満のセルが20%以上ある時には結果は信頼できない

「連続修正」(Yates)

• 検定統計量χ2:「値」6.035
• 自由度df:「自由度」1
• p(≠):「漸近有意確率（両側）」.014

これが出力される時(自由度1)はこちらを採用する

「Fhisherの直接法」

• p(≠):「正確な有意確率（両側）」.014

これが出力される時はこちらを優先するという考え方もある

効果量

Cramer'V:「対称性による類似性」の「CramerのV」「値」.118

Cramer'Vの目安

効果量V	効果の目安
0.5	大
0.3	中
0.1	小
0	なし

残差分析

「クロス表」の各セルの「調整済み残差」の符号

	賛成	反対
女	-2.6	2.6
男	2.6	-2.6

絶対値が1.96より大きければ5%水準で有意

シンタックス

*クロス集計表.
*χ2検定、Phi係数.
*観測値、期待度数、行比率、調整済み残差.
CROSSTABS 
  /TABLES=性別 BY Aという意見に 
  /FORMAT=AVALUE TABLES 
  /STATISTICS=CHISQ PHI 
  /CELLS=COUNT EXPECTED ROW ASRESID 
  /COUNT ROUND CELL.

考察例