統計講座

SPSS 相関と偏相関

量的な変数が複数ある時、この変数間の関係の強度を表す統計量が相関係数である。相関係数は関係の強さと方向性を示す。

被験者諸属性と試験結果(架空データ)を用いる。

ある集団から無作為に選んだ326人に学力テストを行い、その点数を記録し、さらに受験者のさまざまな属性と合わせて結果を分析することにした。

Aさんはその中から受験者の身長と試験結果との関連を分析し、「身長が高ければ、試験で高い点数を取れる」と結論付けた。

このAさんの分析を追試し、批評せよ。

相関係数

データ読み込み後
「分析(A)」→「相関(C)→「2変量(B)」

「分析(A)」→「相関(C)→「2変量(B)」。

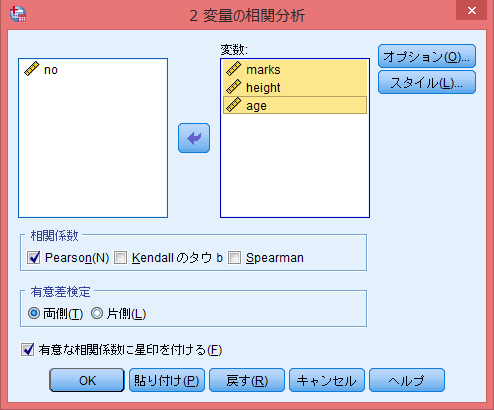
2変量の相関分析
変数
相関関係を調べたい量的変数（間隔・比例尺度）を選択する。
相関係数
順序尺度の時は「Kendall」か「Spearman」を選択。
有意差検定
「両側」

相関分析結果

結果：相関
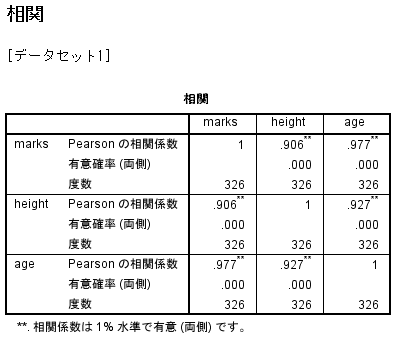
相関係数
  • 点数*身長…r=0.906(p<0.01)
  • 点数*年齢…r=0.977(p<0.01)
  • 年齢*身長…r=0.927(p<0.01)

すべてに正の相関がある。

とりわけ「年齢*身長」に強い相関があることに注目。年齢が高ければ身長も高くなり、点数を引き上げているというモデルが想定できる。そうだとすると身長と点数の関係は疑似相関ということになる。

相関分析シンタックス

*相関行列.
CORRELATIONS 
  /VARIABLES=marks height age 
  /PRINT=TWOTAIL NOSIG 
  /MISSING=PAIRWISE.

偏相関

同じ「年齢」であっても身長と点数に相関があれば、身長と点数の関係には相関関係があるといってよいだろう。そこで「年齢」で統制して「身長」と「成績」の相関関係を調べたい。

このように一つの変数で制御した相関係数を「偏相関係数」と呼ぶ。

「分析(A)」→「相関(C)→「偏相関(R)」

「分析(A)」→「相関(C)→「偏相関(R)」。

偏相関分析
変数
相関関係を調べたい量的変数（間隔・比例尺度）を選択する。
制御変数
影響を制御したい変数を選択する。今回は「年齢」が「成績」「身長」に影響しているのを制御したい。
有意差検定
「両側」

偏相関分析結果

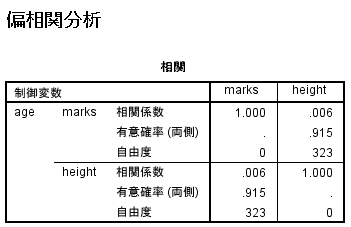
結果：偏相関分析
相関係数
  • 点数*身長…r=0.006(p=915)

年齢で統制した時、点数と身長には相関関係はない(r=0.006)。

偏相関分析シンタックス

*偏相関行列.
PARTIAL CORR 
  /VARIABLES=marks height BY age 
  /SIGNIFICANCE=TWOTAIL 
  /MISSING=LISTWISE.

考察例

Aさんは身長と点数のみで相関係数を求めたが、Aさんは年齢と身長の関係についての考察を行っていない。しかし年齢と身長には非常に高い相関関係が見られた。

そこで身長と点数の関係を年齢で統制して、身長と点数の偏相関係数を求めた。

その結果、身長と点数の相関には有意差が出ない。つまり身長と点数は年齢を媒介とした疑似相関であると言える。このデータから読み取れる結論は「年齢が高い方が試験で高い点を取る傾向がある」と言うことである。

Aさんは疑似相関を真正の相関と見なしたところが間違っている。