SPSS 回帰分析
回帰分析とはある一つの量的変数(結果変数)の値について、一つないしは複数の変数(説明変数)との関係をモデル化する分析手法である。
線型モデルにおいては近似直線の性質、主に傾きから説明(独立)変数と結果(従属)変数の関係を見る。
被験者諸属性と試験結果(架空データ)を用いる。
ある集団から無作為に選んだ326人に学力テストを行い、その点数を記録し、さらに受験者のさまざまな属性と合わせて結果を分析する。得点と身長・年齢・性別の関係について回帰分析を行う。
ダミー変数
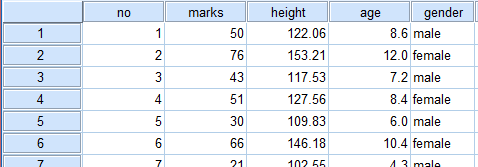
性別genderはカテゴリー変数である。このままでは回帰分析に掛けられない。
この変数を元にダミー変数を作成する。
「変換(T)」→「他の変数への値の再割り当て(R)」
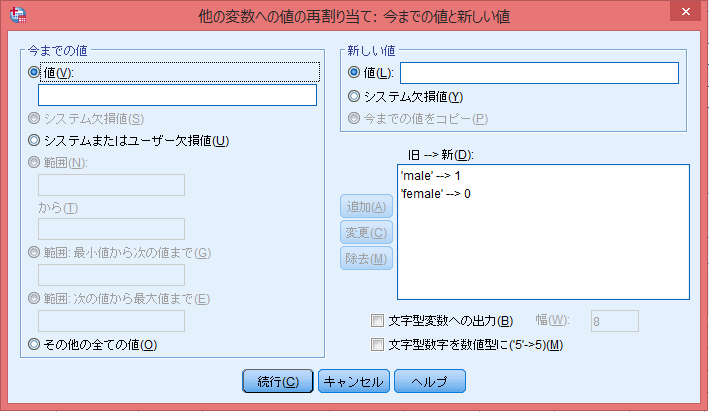
ダミー変数はカテゴリー変数内の各水準を(値)を0または1に置き換えた変数である。水準が3つ以上ある場合は水準ごとに変数を作成する。
今回は「男性・女性」の2値なので、女性→0、男性→1で置き換える。
重回帰分析
「分析(A)」→「回帰(R)→「線型(L)」。
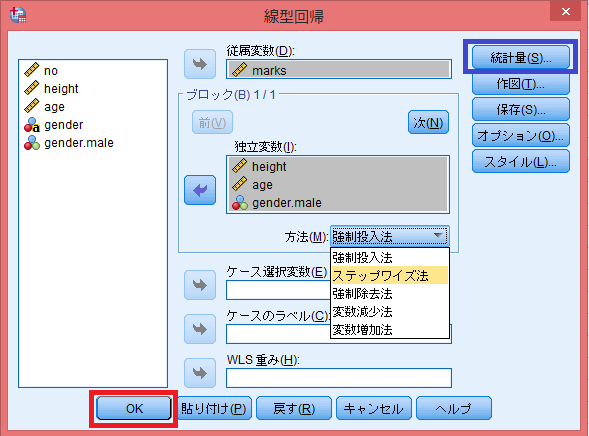
- 従属変数
- 「結果変数」とも呼ぶ。今回はテストの点数を説明するモデルを作りたいので「marks」。
- 独立変数
- 「説明変数」とも呼ぶ。今回はテストの説明を説明するための変数群。カテゴリー変数はダミー変数を用いる。
- 方法
-
- 選択した独立変数すべてを使って回帰分析モデルを立てるのなら「強制投入法」
- 変数選択を行い、モデル最適化を行うのなら「ステップワイズ法」
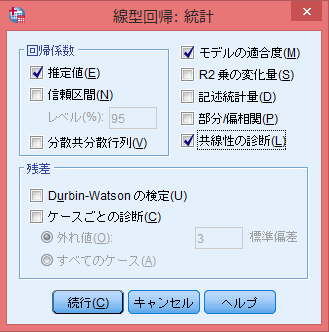
「統計量」をクリック
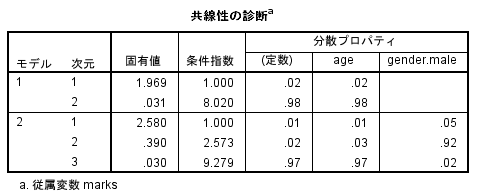
- 多重共線性のチェックをしたいので、「共線性の診断」にチェックを入れる。
結果


- 得点 = a + b*年齢
- 得点 = a + b1*年齢 + b2*性別
SPSSは二つのモデルを提示している。そのどちらを採択するかは分析者の判断による。
「調整済みR2乗」も一つの判断材料だが、絶対的なものではない。
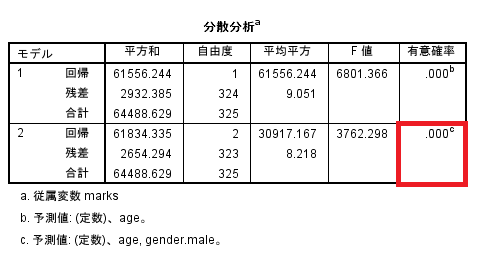
分析者が選択したモデルの有意確率を確認する。0.05未満であればモデルとしては有意。
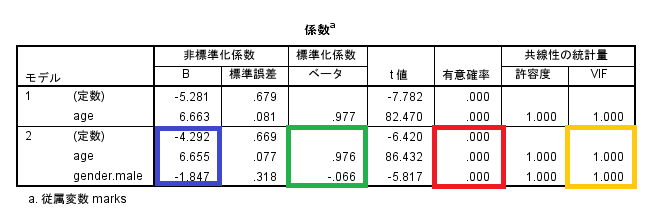
- 偏回帰係数
- 「非標準化係数」の「B」
- 標準化回帰係数
- 「標準化係数」「ベータ」
- 有意確率
- 係数ごとの有意性。0.05未満なら有意
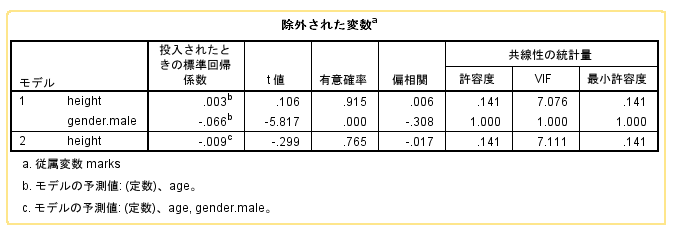
- VIF
多重共線性の確認を行う。10以上なら要注意。
変数選択をやり直すことを検討する。
回帰分析シンタックス
*回帰分析. REGRESSION /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA COLLIN TOL /CRITERIA=PIN(.05) POUT(.10) /NOORIGIN /DEPENDENT marks /METHOD=STEPWISE height age gender.male.
考察例
「得点」を結果変数、「年齢」「身長」「性別」を説明変数とする重回帰分析を行った。
「性別」は男性を1,女性を0とするダミー変数とした上で説明変数に投入し、ステップワイズ法で最適モデルの選択を行った。
説明変数を「年齢」のみとするモデルと「年齢」「性別」とするモデルが候補としてあげられたが、「調整済みR2乗」より「年齢」「性別」モデルを採択した。今回はモデルは複雑であってもなるべく多くの要因の影響をモデル化することを優先した。
重回帰分析の結果は分散分析よりF(2,323)=3763.30,p<.001で有意であった。
偏回帰係数は「年齢」が6.655、「性別(男性)」が-1.847でいずれも有意である。これより年齢が1歳上がれば6.655点上昇し、また男性より女性の方が1.847点高くなる傾向が見られた。