基準値との比較:z検定
- 本章で用いる実習用ファイル
基準値との比較
μ国では大学生のスマートフォンの利用が勉学に悪影響を及ぼしているのではないかと社会問題化している。B大学でも学生のスマートフォン利用時間が増大しているのではないかと懸念が出て、独自に調査することになった。教育省が全国の大学生について1年前に調査した時には平均利用時間180分(分散5,500)であった。今回B大学は全学生の中から500人を無作為抽出を行い、スマートフォン利用時間について調べたところ、下記データが得られた。
| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | No | gender | faculty | time | 平均値 | 分散 | |||
| 2 | 1 | female | science | 193 | 基準値 | 180.00 | 5500.00 | ||
| 3 | 2 | female | law | 166 | A大学 | ||||
| 4 | 3 | male | science | 293 | |||||
| μ国B大学スマートフォン利用時間調査データ | |||||||||
- time(比例尺度)
- D2:D501
このデータより、B大学の学生のスマートフォン利用時間は1年前の全国大学平均と比べて利用時間が長いと言えるだろうか?
結果出力例
| 基準値 | B大学 | |
|---|---|---|
| 平均値 | 180 | 185.83 |
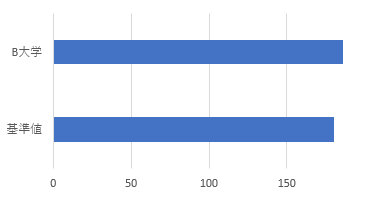
問題1
図表1は平均値と分布 図表1改と同等の結果に見える。ならば同等に結論づけてよいか。
A大学とB大学のスマートフォン利用時間データにおいて、決定的な違いはどこにあるか。
作業
結果出力例
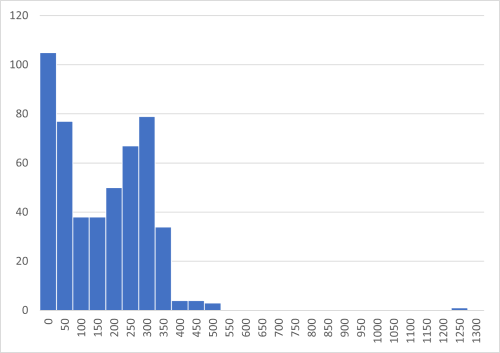
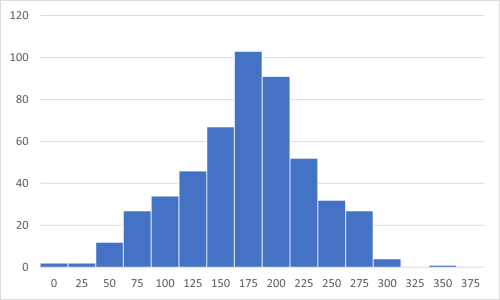
B大学の分布は平均付近を中心とした山型となっており、A大学のデータと異なり、平均値に意味を読み取ることが出来る。
| A大学 | 18507.72 |
| B大学 | 3223.81 |
分散によって平均値の価値が変わる(分布と分散の対応性)。分散が小さいB大学のデータの方が平均値の価値が高い。
問題2
B大学のデータについて、基準値(180分)を上回っていると言えるか。
- Z検定を行い、Z値とp値を求めよ
- 片側検定か両側検定かを判断し、結果を読み取れ(「記述・推測的解釈」)。
- 「有意」と判断(信頼度95%)できた場合は検定結果から読み取れる「主張」を簡潔に記述せよ(「批評的解釈」)。
- 記述・推測的解釈…統計から得られた知見を客観的に記述する。
- 批評的解釈…統計的知見を「根拠」として、文脈に合わせて自由に議論を進める。
主張テンプレート
…トピックセンテンス(主張)…。B大学学生のスマートフォン平均利用時間(サンプル平均時間○)は1年前の全国平均(180.00)より[長い/短い](Z=●, p<.05)。補足説明文など。
…(以下、批評的解釈に基づく主張)
Z検定
統計的検定の基本は「そんな結果になるのは偶然ではあり得ない」ことを示すことである。
今回の場合だと「基準値を母平均が上回っている」という仮説(調査仮説)を直接論証することは出来ない(母平均は不明だから)。「母平均は基準値を上回っているわけではない」(帰無仮説)のなら、現に得られた標本平均がそんな値を取ることは偶然ではあり得ない、ことを論証する。
- いいたいこと:調査仮説=対立仮説(alternative hypothesis)
-
比較対象の全国平均(基準値)180をB大学学生調査の母平均は上回っている
←直接的には確定できない(母平均が分からないから)
←確率計算も出来ない(母平均は不動であって、基準値と異なるかどうかは既に確定しているから)
- 嫌なツッコミ:帰無仮説(null hypothesis)
-
- 比較対象の全国平均(基準値)180をB大学学生調査の母平均は上回るとは言えない
- サンプル平均では上回っているように見えたとしても、それは偶然で片付けられる範囲内である
←ここに初めて確率論が登場する!
サンプルは理論上何度も取り直せ、その都度異なった平均値(標本平均)が算出できる。つまり確率計算ができる。
- ツッコミには倍返しだ!:帰無仮説を棄却するためになすべきタスク
-
-
母平均が基準値180を上回らないとすると、実際に集めて得られた標本平均が偶然(基準値180を上回る)185.83なんて値を取る確率(p値)は極めて低い
「標本平均が母平均とそんなにかけ離れた値を取るなんておかしい」
-
「だったら実際の母平均は180なんかじゃなくて、もっと標本平均に近い値だったんだ!」:ミッションコンプリート
-
- 証明するべき事柄
-
基準値180と標本平均の差が偶然では起こりえないだけの大きなものであるということ
母平均180と標本平均の差が生じる確率は偶然と見なせる確率(=有意水準)より小さい
- 平均差を確率に変換する装置
-
標本平均の分布←平均差(x軸)と確率(y軸)を変換する
- 正規分布
- 中心極限定理

- x軸:無作為抽出を何回も繰り返して得られた標本平均群
- y軸:無作為抽出された標本の平均値(標本平均)が特定の値を取る確率
- 標本平均分布の性質
-
- 標準正規分布:原点と特定の値との差が生じる確率がすべて計算済み
- 今分析しているデータの標本平均の分布は標準正規分布に規模(分布の散らばりの大きさ=標本平均の分布の標準偏差)を加えたもの。
- 標本平均の分布の標準偏差→標準誤差
平均差と分布の標準偏差(標準誤差)が分かればそれ以上の平均差が生じる確率(p値)が分かる
Z検定の計算
- 有意水準はあらかじめ定めておく(一般的には5%)。
F G 16 有意水準 5% - 平均差 = AVERAGE(time) - 基準値(180)
F G 17 平均差 =AVERAGE(time) - G2 - 標準誤差 = SQRT(基準値の分散 / サンプルサイズ)
サンプルサイズが母集団の総数と一致すれば分布の分散は最小、サンプルサイズが1であれば母集団の分散と同程度の分散になる(最大)→サンプルサイズが大きくなればなるほど分布の散らばり(標準誤差)は小さくなる
F G 18 標準誤差 =SQRT(H2/COUNT(time)) - Z値(検定統計量) = 平均差 / 標準誤差
標本から導かれた平均差を、確率計算するのに必要な標準正規分布の規模に換算する。
Z値(検定統計量):標準正規分布における標本平均と基準値の差
F G 17 平均差 5.83 18 標準誤差 3.32 19 Z値 =G17/G18 - p値は標本の平均値と基準値との大小に関する仮説から3つ(>, <, ≠)計算する
p値は標本の平均が基準値(帰無仮説における母平均)に対してそれだけ距離を持つ確率
- 片側検定:p値(母平均>基準値)
-
- 帰無仮説
- 母平均が基準値を上回らない。
標本平均と母平均との差がz値より正の方向にズレる確率 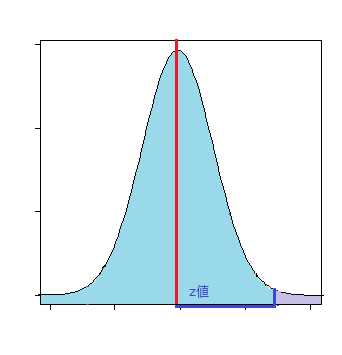
p値 = 1 - NORM.S.DIST(Z値, TRUE)
- 片側検定:p値(母平均<基準値)
-
- 帰無仮説
- 母平均が基準値を下回らない。
標本平均と母平均との差がz値より負の方向にズレる確率 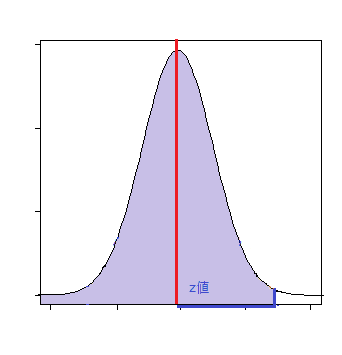
p値 = NORM.S.DIST(Z値, TRUE)
- 両側検定:p値(母平均≠基準値)
-
- 帰無仮説
-
- z値>0…母平均は基準値を上回らない
- z値<0…母平均は基準値を下回らない
標本平均と母平均との差の絶対値がz値より正の方向にズレる確率 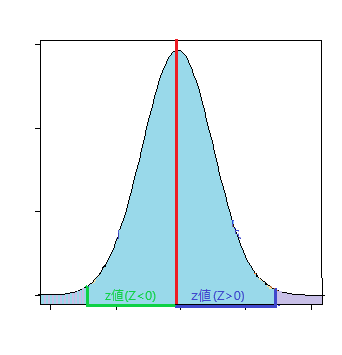
p値 = (1 - NORM.S.DIST(ABS(Z値),TRUE))*2
F G 19 Z値 1.76 21 p値(≠) =(1-NORM.S.DIST(ABS(G19),TRUE))*2 22 p値(>) =1-NORM.S.DIST(G19,TRUE) 23 p値(<) =NORM.S.DIST(G19,TRUE) - 棄却値 = NORM.S.INV(1 - 有意水準/2)
標準正規分布における有意水準に対応する平均差(平均差がこの値より大きくなるとその平均差は偶然では片付けられないと見なす)。
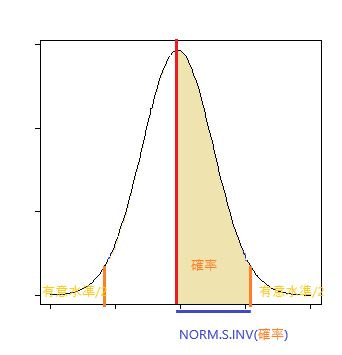
F G 16 有意水準 5% 20 棄却値 =NORM.S.INV(1 - G16/2)
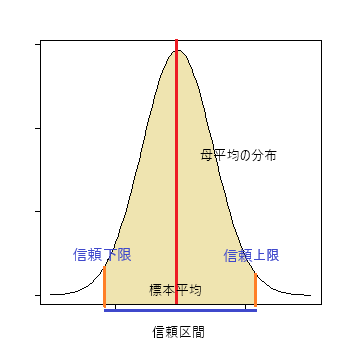
信頼区間
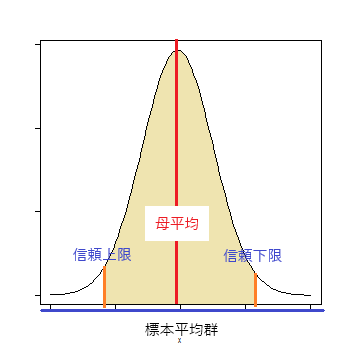
標本平均と基準値との距離が有意水準より大きい確率(オレンジ色の面積)内に収まる時、この平均値の範囲をもって「母平均の信頼区間」とする。
標本平均がオレンジ色の面積の左端に来た時、母平均(赤線)は上限となり、標本平均が右端に来た時、母平均は下限となる。
※この分布は標本平均の分布であって、母平均の分布ではない。
- 信頼上限 ← 標本平均 + 棄却値 * 標準誤差
- 信頼下限 ← 標本平均 - 棄却値 * 標準誤差
| F | G | |||
|---|---|---|---|---|
| 18 | 標準誤差 | 3.32 | ||
| 20 | 棄却値 | 1.96 | ||
| 24 | 信頼上限 | =AVERAGE(time) + G20*G18 | ||
| 25 | 信頼下限 | =AVERAGE(time) - G20*G18 | ||
有意水準α=0.05としたとき、この信頼区間を95%信頼区間と呼ぶ。このときの95%とはA「母平均がその範囲に95%の確率で収まる」ということを意味しない。そうではなくて、B「この信頼区間が母平均を含む比率は95%である」といっているに過ぎない。
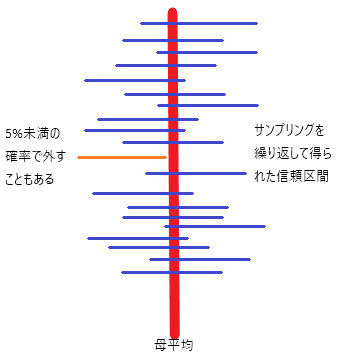
なにが違うのか?母平均に関する情報量はAの方が多いのである。残念ながらこの統計理論の枠組みでは母平均自体の確率云々は語り得ない。95%とは母平均に関する確率ではなくて、調査の精度を示している指標に過ぎないのだ。
結果
| F | G | |||
|---|---|---|---|---|
| 5 | サンプルサイズ | 500 | ||
| 6 | 平均値 | 185.83 | ||
| 7 | 中央値 | 186.00 | ||
| 8 | 最頻値 | 187.50 | ||
| 9 | 最大値 | 358.00 | ||
| 10 | 最小値 | 5.00 | ||
| 11 | 範囲 | 353.00 | ||
| 12 | 分散 | 3223.81 | ||
| 13 | 標準偏差 | 56.78 | ||
| 15 | z検定 | |||
| 16 | 有意水準 | 5% | ||
| 17 | 平均差 | 5.83 | ||
| 18 | 標準誤差 | 3.32 | ||
| 19 | Z値 | 1.76 | ||
| 20 | 棄却値 | 1.96 | ||
| 21 | p値(≠) | 0.08 | ||
| 22 | p値(>) | 0.04 | ||
| 23 | p値(<) | 0.96 | ||
| 24 | 信頼上限 | 192.33 | ||
| 25 | 信頼下限 | 179.33 | ||
今回調査は「スマートフォン利用時間が長すぎる」ことへの懸念が問題となって行われている。つまりB大学が基準値を上回っているかどうかが問われているのである。基準値と差があると言えない、あるいは下回っているのであれば特に問題にはならず、話はそこで終了である。ということでここでは片側検定(B大学>基準値)を用いることが出来る。もしB大学が基準値を上回っているか、下回っているか、両方を検知しなければならないのであれば、両側検定を用いなければならず、今回は帰無仮説を棄却できなかった(有意性を得られなかった)。
主張
Z検定の結果から得られた知見をまとめよ。
-
全国水準でなされた学生のスマートフォン利用時間が長すぎるという懸念に関して、B大学学生も当てはまる。B大学学生のスマートフォン平均利用時間(サンプル平均185.83)は1年前の全国平均(180.00)より長い(Z=1.76, p<.05)。早急に教育省に対して調査報告並びに今後の指針説明を行う準備を進める必要がある。
課題
μ国の全大学生のスマートフォン平均利用時間は180分(分散5,500)である。B大学は全学生の中から500人を無作為抽出を行い、スマートフォン利用時間について調べたところ、下記結果が得られた。
| 基準値 | B大学 | |
|---|---|---|
| 平均値 | 180 | 185.83 |

この結果より、B大学の学生のスマートフォン利用時間は1年前の全大学生平均と比べて利用時間は長いと言えるだろうか?
ヒント:B大学の結果を見てから、「長い」かどうかが問題として提示されている。
-
B大学学生のスマートフォン平均利用時間が1年前の全国平均(180.00)と差があるとは言えない。今回の調査で得られた標本の平均利用時間は185.83であったが、Z検定(両側)より5%水準で有意性が得られなかった(Z=1.76, p=.08)。