統計講座

クロス集計と独立性の検定

カテゴリー変数同士の関係を見る際には数を数えるというのがまずなすべきことである。複数のカテゴリー間で度数を示したものがクロス集計表である。分散分析で登場したクロス集計表と異なり、カテゴリ変数しかないので、情報量は限られている。

クロス集計表自体は単純な記述統計だが、その有意性の検証にはノンパラメトリック検定であるχ2検定を用いる。

μ国で有権者を対象に政治意識調査を行った。調査は無作為抽出で対象者を選び、500人から回答を得られた。

問1 あなたの性自認(Gender)は何ですか。

男性(male)
女性(female)

問2 あなたの住所登録がなされている府(Prefecture)はどこですか。

Morn
Angerm
Juic
Magnol
Camell
Beyond

問3 あなたの支持政党(Party)は何党ですか。

保守党(Conservative)
民主党(Democratic)
特になし(unaffiliated)

問4 あなたは現内閣を支持(CabinetSupport)しますか。

支持する(Yes)
支持しない(No)

この調査から得られたデータより、現住所(Prefecture)と支持政党(Party)との関連に付いて得られる知見を述べよ。

No	Gender	Prefectures	Party	CabinetSupport
1	female	Camell	unaffiliated	No
2	female	Morn	unaffiliated	No
3	male	Magnol	unaffiliated	Yes
4	male	Angerem	unaffiliated	No
5	female	Magnol	unaffiliated	Yes
6	male	Morn	Conservative	Yes
7	male	Camell	Democratic	No

μ国政治意識調査

クロス集計

data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/chiSq.Test.Independence.csv")
summary(data)
group <- data$Gender
answer <- data$CabinetSupport

crossTable <- table(group,answer) #クロス集計表
addmargins(crossTable)
N <- sum(crossTable) #サンプルサイズ

#割合計算
print(group.prop <- prop.table(crossTable,margin=1)) #行比率
print(answer.prop <- prop.table(crossTable,margin=2)) #列比率

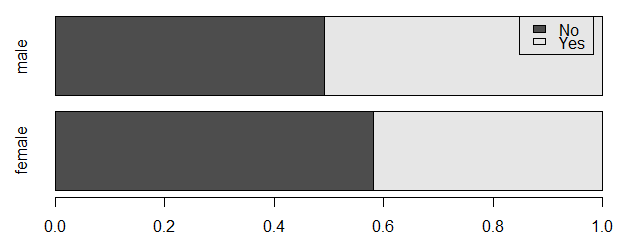
#行比率の表に対する帯グラフ
barplot(t(group.prop), horiz=T, legend=colnames(group.prop))

table(行,列)

度数分布表・クロス集計表(matrix)を作る。

addmargins(A)

行列の周辺度数を計算して表に加える。

A=行列(matrix)データ

prop.table(matrix,margin)

比率計算を行う。

x=行列(matrix)データ
margin=比率計算の方向(1…行比率、2…列比率、省略…全体比率)

観測値
	No	Yes	Sum
female	149	107	256
male	120	124	244
Sum	269	231	500

行比率
	No	Yes
female	58.2%	41.8%
male	49.2%	50.8%

χ2検定

このクロス集計表で性自認と内閣支持不支持に関連があることを読み取って良いかどうかを検証したい。

いいたいこと:対立仮説

性自認と内閣支持不支持に関連がある

帰無仮説

性自認と内閣支持不支持には関連がない(相互に独立している)。関連があるように見えたとしても、それはサンプルの偏りから偶然に生じる誤差の範囲内である。

帰無仮説を棄却する根拠

完全に行(住所)と列(支持政党)が独立したクロス表と比べて、現実のクロス表(観測値)のセルごとの値はあまりにもズレが大きすぎる。こんなにズレが出るのは偶然ではあり得ない。何かしら必然的な理由(性自認と内閣支持不支持に関連がある)があるのだ!

証明するべき事柄

相互に独立したクロス表の各セルの値と観測値との差の合計が偶然では起こりえないだけの大きなものであるということ

この差が生じる確率は偶然と見なせる確率(=有意水準)より小さい

標準化残差の計算

expected.crossTable <- apply(crossTable,2,function(x){sum(x)*apply(crossTable,1,sum)/N}) #期待値
res.crossTable <- crossTable - expected.crossTable #残差
std.res.crossTable <- res.crossTable/sqrt(expected.crossTable) #標準化残差

表(matrix)を行単位・列単位に計算したい時にはapply関数を用いる。

apply(x,margin,function)

x=表(matrix)データ
margin=1なら行、2なら列に対して関数を適用する
function=関数定義または関数名

期待値
	No	Yes
female	137.7	118.3
male	131.3	112.7

残差
	No	Yes
female	11.3	-11.3
male	-11.3	11.3

標準化残差
	No	Yes
female	0.96	-1.03
male	-0.98	1.06

期待値(帰無仮説=性自認と内閣支持不支持が完全に独立している状態)

観測値はカテゴリ(性自認)の違いの影響により、数値(内閣支持率)が動いている(と見なす)。そうしたカテゴリー間の違いが生じないように(性自認と内閣支持率が相互に独立しているように)統制した状態を元の理想状態とする。これを「期待値」と呼ぶ。

行方向の周辺度数×列方向の周辺度数/合計の周辺度数

期待値の計算
	No	Yes	合計
female	256*269/500		256
male			244
合計	269	231	500

残差(帰無仮説にもとづく期待値と観測値とのズレ)

観測値 - 期待値(元データ)

標準化残差(サンプルサイズの影響を除去)

データ一件一件のズレの大きさ（偏差平方←（観測値-期待値)^2））を元データ(期待値)で割ったものが「元データからの標本データの散らばり」である。これの平方根を取ったものが「標準化残差」。

χ2値とp値

chisq.df <- (nrow(crossTable) - 1)*(ncol(crossTable) - 1) #自由度
chisq.value <- sum(std.res.crossTable^2) #χ2値
p.value <- 1 - pchisq(chisq.value,chisq.df) #p値

自由度
	No	Yes	Sum
female	149	107	256
male	120	124	244
Sum	269	231	500

標準化残差^2
	No	Yes
female	0.9225283	1.0742863
male	0.9678986	1.1271200

自由度(クロス表の大きさ)

周辺度数を固定したとき、数値を自由に設定できるセル数。

χ2値(表全体のズレの大きさ)

4.091833 ← sum(0.9225283,0.9678986,1.0742863,1.1271200)

セルごとの「元データからの標本データの散らばり」(標準化残差^2)の総和を散らばりの度合いに関する検定統計量とする。χ2値はχ2分布に従う。

Peasonのχ2検定に対する批判

Peasonのχ2検定は離散量である度数に対する検定を連続量に対する確率分布であるχ2分布で行っている。従ってそこから得られる有意確率は近似値に過ぎず(漸近有意確率)、特に期待度数が小さいときにはそのズレは大きくなる。

Fisherの正確確率

クロス集計表のセルごとの値は離散量(度数:0以上かつ整数)であるため、有限であり、周辺度数が固定されている時には、その生起確率は正確に計算できる。それがFisherの正確確率である。

RにはFisher正確確率を計算する関数が用意されている。ただしデータ数が大きくなるとプログラムが止まるので注意。

fisher.test(crossTable)

ちゃぶ台返し

セルごとの値が度数であるが故に正確な確率が計算可能であるというのは「周辺度数が固定されている」ことを前提とした話である。Fisherの正確確率検定が正確なのはその条件の下においてである。

確かに理系分野の実験においては周辺度数を固定する、というのはあり得べきことである。しかし社会科学において周辺度数は固定されていると見なすべきだろうか？

内閣を支持するかしないかを男女別に比較する調査を行ったとしよう。このときの周辺度数は「男女併せた内閣支持率」である。これは固定されているものだろうか。全体の支持率自体も変動するし、それもまた興味の対象である。つまり周辺度数を固定しているものと見なすことは出来ない。

周辺度数も変動するとすると、期待度数を連続数と見なしたPeasonχ2検定の結果が著しい歪みを生じさせているとは言えない。

実験

Peasonのχ2検定、Yates補正、そしてFisherの正確確率検定、各々である特定のp値をどの頻度で出しているかを視覚化してみる。

自由度1のクロス表を対象とし、指定された1行目の比率と1列目の比率からクロス表をランダムに繰り返し生成する。そしてその有意確率をPeason、Yates、Fisherの各方法で計算し、その登場頻度をグラフにする。

今回は期待度数5以下のセルが登場するようにサンプルサイズと各セルの比率を指定した。

source("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/compare.chisq.fisher.test.R", encoding="UTF-8")
compare.chisq.fisher.test(0.1,0.2,N=50,condition=T,lim=0.1) #周辺度数を固定する
compare.chisq.fisher.test(0.1,0.2,N=50,condition=F,lim=0.1) #周辺度数を固定しない

x軸はp値、y軸はx以下のp値の出現率である。理想的にはy = xの直線と一致する。それより上側に出ると、その時点まででp値の安売り、下回るとp値の出し惜しみということである。0.05時点で直線の上にいれば有意でないものを有意判定をおこなっており、第一種過誤を引き起こしている。一方下にいれば、有意性に対してより厳しい判定をしている、第二種過誤を引き起こしているということ。第一種過誤の方が罪は重いので、下にいる方が望ましい。

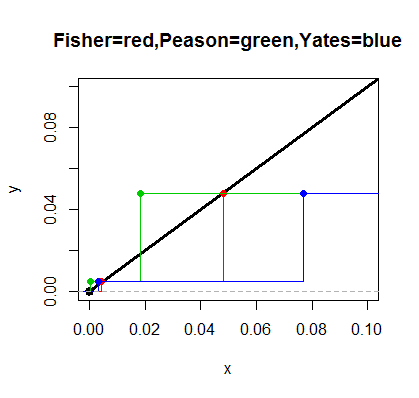
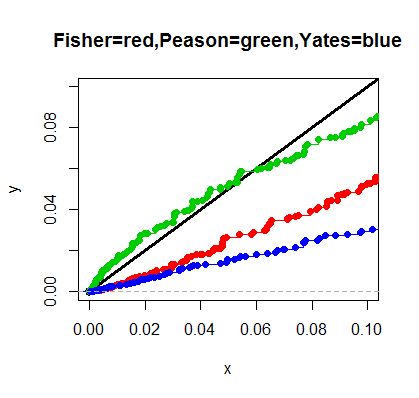
結果は試行するごとに変わる。

周辺度数を固定した場合、Fisherの正確検定は y = x上にほぼ乗るが、Peasonのχ2検定はそれより上にずれるケースが多発する。Yates補正すると y = xより下になる。

一方周辺度数を固定しない場合、Peasonのχ2検定はほぼy = x線上に乗る。ただし一定の割合でp値を安売りする(y = xより上側に膨らむ）。特にサンプルサイズが小さいとリスクは大きくなる。一方サンプルサイズが大きくなると、全体としてはPeasonのχ2検定が一番y = xに近似した分布を取るようだ（他の二つは下に沈み込む傾向が強い）。

残る問題

というわけでなにがなんでも正確確率検定を用いるのが正しい、というわけでもない。しかし以下の2点においてはPeasonのχ2検定の結果の歪みは大きくなるとされている。

期待度数の中に5以下のセルがある: セルごとの期待度数が十分多いときには連続量と同等と見なせて、χ2分布は実際の生起確率に近似した値を取る(漸近有意確率)。しかし期待度数が不足（期待度数5以下）していると、結果が歪んでしまう。
クロス集計表の自由度が1である: χ2分布は自由度によって形を変えるが、自由度1のときには歪な曲線を描く。したがって自由度1のクロス集計表では適当な結果が得られない。

この問題への対処法

期待度数が5以下のセルがある: Fisherの正確確率検定
クロス集計表の自由度が1である: Yatesの補正(連続修正）

Yatesの補正

1 - pchisq(chisq.value,chisq.df)
fisher.test(crossTable)

0.04309 ← 1 - pchisq(chisq.value,chisq.df) #Peasonのχ2検定値
0.04846 ← fisher.test(crossTable) #Fisherの正確確率

χ2分布を用いたPeasonの検定とFisherの正確確率検定ではPeasonの方がp値が小さい。これは第一種過誤をもたらす危険性がある。自由度が小さいとこのズレが大きくなる傾向がある。特に自由度1(2*2のクロス表)のときには補正をしたほうがよい。

この補正をするための方法がYatesの補正である。

yates.std.res.crossTable <- (abs(res.crossTable) - 0.5)/sqrt(expected.crossTable) #Yatesの補正
yates.std.res.crossTable[which(yates.std.res.crossTable < 0)] <- 0 #補正後の値が0未満なら0にする
yates.chisq.value <- sum(yates.std.res.crossTable^2) #χ2値
yates.p.value <- 1 - pchisq(yates.chisq.value,chisq.df) #p値

0.05322388 ← Yates補正したp値

Peason検定のときよりも大きい値になっている。つまり補正前よりも第一種過誤が減るわけだ。

χ2検定使い分けの一案

周辺度数を固定(実験系など)

Fisherの正確確率

周辺度数を固定しない(社会調査など)

期待度数<=5セルあり

Fisherの正確確率

すべてのセルが期待度数>5

自由度=1: Yates補正
自由度>1: Peasonのχ2検定

効果量 CramerのV値

v.value <- sqrt(chisq.value/(N*(min(nrow(crossTable),ncol(crossTable))-1))) #Cramer'V

χ2値はサンプルサイズによって変化する。その影響を排除し、クロス表の大きさ（自由度）の影響を補正したものが効果量 CramerのV値である。

0.09046362

効果があるとは言いづらい結果である。

残差分析

se.crossTable <- sqrt(apply(crossTable,2,function(x){(1 - sum(x)/N )*(1 - apply(crossTable,1,sum)/N)})) #標準誤差
adj.res.crossTable <- std.res.crossTable/se.crossTable #調整済み標準化残差
res.p.crossTable <- (1 - pnorm(abs(adj.res.crossTable)))*2 #残差のp値

χ2値はズレの大きさのみを問題にしてきたが、それで有意性が確認できれば、次にセルごとにどういう方向にずれているかを検討することになる(自由度1のクロス集計表では意味がないが、本項での計算式は自由度2以上のクロス集計表でもそのまま使える)。

「標準化残差」のセルごとの値の符号(+-)から結果を読み取る。

この残差を検定統計量Z値にしたものが「調整済み標準化残差」（標準化残差/標準誤差=Z値）である。ここから正規分布を用いてp値が計算される。

期待値(再掲)
	No	Yes
female	137.7	118.3
male	131.3	112.7

標準誤差
	No	Yes
female	sqrt((1-256/500)*(1-269/500))=0.47	sqrt((1-256/500)*(1-231/500))=0.51
male	sqrt((1-244/500)*(1-269/500))=0.49	sqrt((1-244/500)*(1-231/500))=0.52
※SQRT(当該セルを含まない横周辺和比率*当該セルを含まない縦周辺和比率)

標準化残差(再掲)
	No	Yes
female	0.96	-1.03
male	-0.98	1.06

調整済み標準化残差
	No	Yes
female	-2.02	2.02
male	2.02	-2.02

p値
	No	Yes
female	0.04	0.04
male	0.04	0.04

p値が有意水準(0.05)を下回っているセルが有意である。

今回はすべてのセルが有意(p<0.05)である(自由度が1のときにはすべてのセルのp値はPeasonχ2検定のp値になる)。

これにより女性は「支持しない」、男性は「支持する」と回答する傾向があると言える(ただしYates検定ではクロス表自体が有意ではない)。

Rでのクロス集計表独立性検定

R標準の機能として、chisq.test()が用意されている。引数に自由度1のクロス集計表を入れるとデフォルトではYates補正を行う。

data <- read.csv("http://kyoto-edu.sakura.ne.jp/weblesson/statistics/data/chiSq.Test.Independence.csv")
summary(data)
group <- data$Gender
answer <- data$CabinetSupport

crossTable <- table(group,answer) #クロス集計表

#χ2検定
#Peason
chisq.test(crossTable,correct=FALSE) #2*2の集計表の時はcorrect=FALSEを指定しないとYates補正が行われる
#Yates補正
print(chisq.result <- chisq.test(crossTable) )

#標準化残差
chisq.result$residuals

#調整済み標準化残差
chisq.result$stdres